Introdução ao Heap Sort em C
A classificação é uma técnica que trata principalmente da ordem dos elementos com base em diferentes propriedades. (Propriedades como organizar dados em ordem crescente, decrescente ou alfabética). Um exemplo importante de classificação que podemos pensar aqui é a ordenação de itens durante as compras online. Podemos nos relacionar com preços, popularidade, mais recentes e assim por diante. Portanto, existem muitas técnicas para esse posicionamento de elementos através da classificação. Neste tópico, vamos aprender sobre a Classificação de pilha em C.
Aqui vamos aprender uma das técnicas de classificação mais comuns, Heap Sort, através da linguagem de programação C.
A lógica para Heap Sort
Como realmente podemos executar a classificação de heap? Vamos conferir abaixo.
Em primeiro lugar, o heap é uma das estruturas de dados baseadas em árvore. A árvore envolvida aqui é sempre uma Árvore Binária Completa. E existem dois tipos de pilha
- Min - Heap: geralmente organizado em ordem crescente, ou seja, se o elemento do nó pai tiver um valor menor que o dos elementos do nó filho.
- Max - Heap: geralmente organizados em ordem decrescente, ou seja, se o elemento do nó pai tiver um valor maior que o dos elementos do nó filho.
Etapas para a classificação de heap
- Depois que um dado de lista não classificado é obtido, os elementos são organizados na estrutura de dados do heap, com base na criação de um min-heap ou max-heap.
- O primeiro elemento da lista acima é adicionado à nossa matriz
- Novamente, formando a técnica de estrutura de dados principal, da mesma maneira que o primeiro passo é seguido, e novamente o elemento mais alto ou o menor elemento é escolhido e adicionado à nossa matriz.
- Etapas repetidas nos ajudam a obter a matriz com a lista classificada.
Programa para Heap Sort em C
#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)#include
int main()
(
int h(20), num, i, j, root, t, x;
printf("Enter number of elements :");
scanf("%d", &num);
printf("\nEnter the elements : ");
for (i = 0; i < num; i++)
scanf("%d", &h(i));
// build max heap
for(i=0;i (
x=i;
do
(
root = (x - 1) / 2;
if (h(root) < h(x))
(
t = h(root);
h(root) = h(x);
h(x) = t;
)
x = root;
) while (x != 0);
)
printf("Heap array formed is: ");
for (i = 0; i < num; i++)
printf("%d\t ", h(i));
for (j = num - 1; j >= 0; j--)
(
t = h(0);
h(0) = h(j);
h(j) = t;
root = 0;
do
(
x = 2 * root + 1;
if ((h(x) < h(x + 1)) && x < j-1)
x++;
if (h(root) (
t = h(root);
h(root) = h(x);
h(x) = t;
)
root = x;
) while (x < j);
)
printf("\nThe sorted array is : ");
for (i = 0; i < num; i++)
printf("\t %d", h(i));
)
Primeiro, solicitamos que o usuário insira o número de elementos necessários para classificação e, em seguida, o usuário tem permissão para inserir diferentes elementos que devem ser classificados.
Etapas seguidas
- O próximo em que estamos focando é criar uma matriz de heap, nesse caso, matriz de heap max.
- A principal condição para obter uma matriz de heap máximo é verificar se nenhum valor do nó pai é menor que o valor do nó filho. Vamos trocar até alcançarmos essa condição.
- A principal vantagem nessa árvore binária completa é que os nós filhos esquerdo e direito de um nó pai podem ser acessados com os valores 2 (i) + 1 e 2 * (i) + 2, respectivamente. Onde i é o nó pai.
- Então, por esse caminho aqui, estamos colocando nosso nó raiz que contém o valor máximo no local do nó folha mais à direita. E, novamente, seguindo o mesmo procedimento, de modo que o próximo número máximo agora se torne o nó raiz.
- Vamos seguir o mesmo procedimento até que apenas um nó seja deixado na matriz de heap.
- E então, estamos organizando nossa matriz de heap para formar uma matriz classificada perfeita em ordem crescente.
- Finalmente, estamos imprimindo a matriz classificada na saída.
Resultado:
A saída está anexada abaixo.
Deixe-me mostrar a representação pictórica dos acontecimentos:
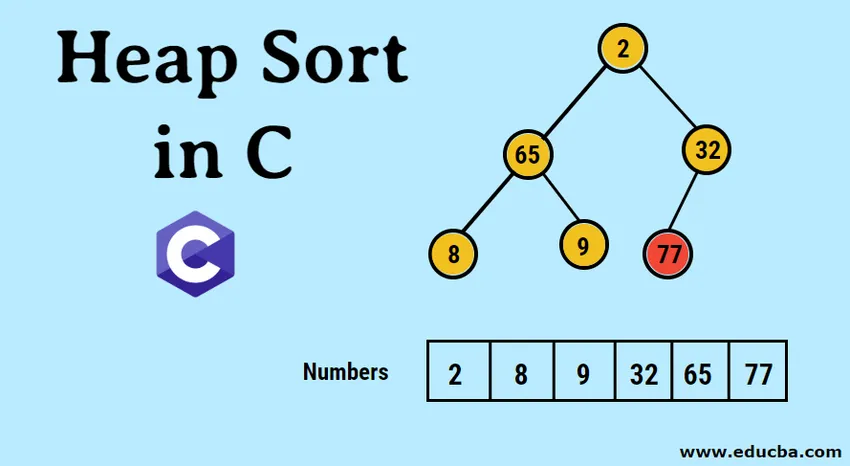
- Os dados inseridos são representados primeiro na forma de uma matriz unidimensional da seguinte maneira.

- A representação pictórica da árvore binária formada é a seguinte:
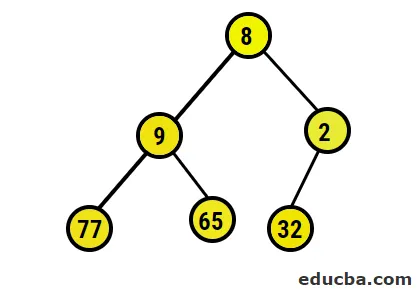
- Agora, vamos converter para o heap máximo, certificando-se de que todos os nós pais sejam sempre maiores que os nós filhos. Conforme mencionado na saída na matriz classificada em heap, a representação pictórica seria:
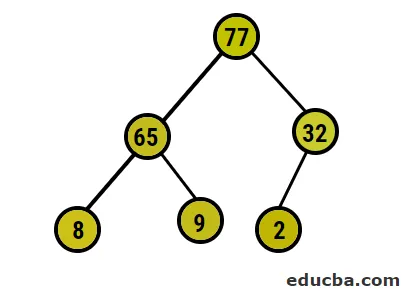
- Depois disso, vamos trocar o nó raiz pelo extremo da folha e excluí-lo da árvore. O nó folha seria a raiz agora e novamente o mesmo processo e seguido para obter novamente o elemento mais alto na raiz
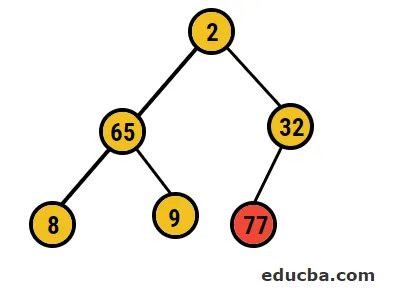
- Portanto, nesse caso, 77 dígitos estão sendo excluídos dessa árvore e colocados em nossa matriz classificada e o processo é repetido.
Acima, vimos isso para formar a matriz heap máxima. O mesmo processo também é tratado com a formação da matriz min-heap. Como discutido acima, a única diferença está no relacionamento entre os elementos do nó pai e filho.
Como exercício, você pode tentar formar a classificação da pilha na ordem decrescente?
Conclusão
Embora existam muitas técnicas de classificação, a classificação de heap é considerada uma das melhores técnicas de classificação devido à sua complexidade de tempo e espaço. A complexidade de tempo para todos os casos melhores, médios e piores é O (nlogn), onde a complexidade do pior caso é melhor que a complexidade do Quicksort e a complexidade do espaço é O (1).
Artigos recomendados
Este é um guia para a Classificação de Heap em C. Aqui discutimos a lógica e as Etapas para a Classificação de Heap com o código de exemplo e a saída juntamente com as representações pictóricas. Você também pode consultar os seguintes artigos para saber mais -
- Heap Sort In Java
- Seleção Classificar em Java
- Palíndromo no programa C
- Padrões em Programação C
- Classificação de heap em C ++ (algoritmo)
- Heap Sort em Python
- Multiplicação de matrizes de programação C