
Diferença entre Z score vs T score
A pontuação Z é uma conversão de dados brutos em uma pontuação padrão, quando a conversão é baseada na média da população e no desvio padrão da população. Quando um conjunto de dados completo está disponível conosco, podemos calcular a pontuação Z. O escore Z é a subtração da média da população do escore bruto e depois divide o resultado pelo desvio padrão da população. A pontuação T é uma conversão de dados brutos para a pontuação padrão quando a conversão é baseada na média da amostra e no desvio padrão da amostra. Quando o conjunto de dados da população não está disponível, precisamos coletar alguns dados da amostra para calcular a média da amostra e o desvio padrão da população.
Escore Z
Sob uma distribuição normal, onde os dados completos estão disponíveis, é uma distância da média. Sua fórmula é a seguinte,
Z= (x-μ)/σ
Onde,
X = dados brutos individuais
μ = Média da população
σ = desvio padrão da população
Pontuação T
A pontuação T é a subtração do desvio padrão individual da média individual e, em seguida, divide o resultado com o desvio padrão da amostra, resultado inteiro multiplicado pelo tamanho da amostra. Sua fórmula é a seguinte,
t = ((- μ)/s)*
= média da amostra
μ = Média da população
s = Desvio padrão da amostra
n = tamanho da amostra
Vamos dar um exemplo para entender o mesmo de uma maneira melhor:
Em um artigo, existem três subdivisões: I, II e III. Deixe o número de alunos que responderam corretamente ser 25%, ou seja, 75% não poderão responder corretamente. Da mesma forma, deixe 10% e 20% pelo número de pessoas que responderam corretamente as seções II e III; assim, 90% e 80% encontraram as seções II e III. Assumimos que a capacidade medida por esses três itens é a mesma e é normalmente distribuída,
A pontuação de cada aluno de uma turma é usada para calcular a média de notas igual a 50 e um desvio padrão de 10. Podemos calcular a pontuação Z com a pontuação de 50 como (50-50) / 10 = 0
Podemos interpretar que a pontuação do aluno está a 0 distância (em unidades de desvios padrão) da média, portanto o aluno obteve uma média.
Se a pontuação for 60, a pontuação Z é (60-50) / 10 = 1
Podemos interpretar que o aluno obteve pontuação acima da média - uma distância de 1 desvio padrão acima da média.
Comparação cara a cara entre o escore Z vs o escore T (Infográficos)
Abaixo está a diferença top 9 entre Z score vs T score 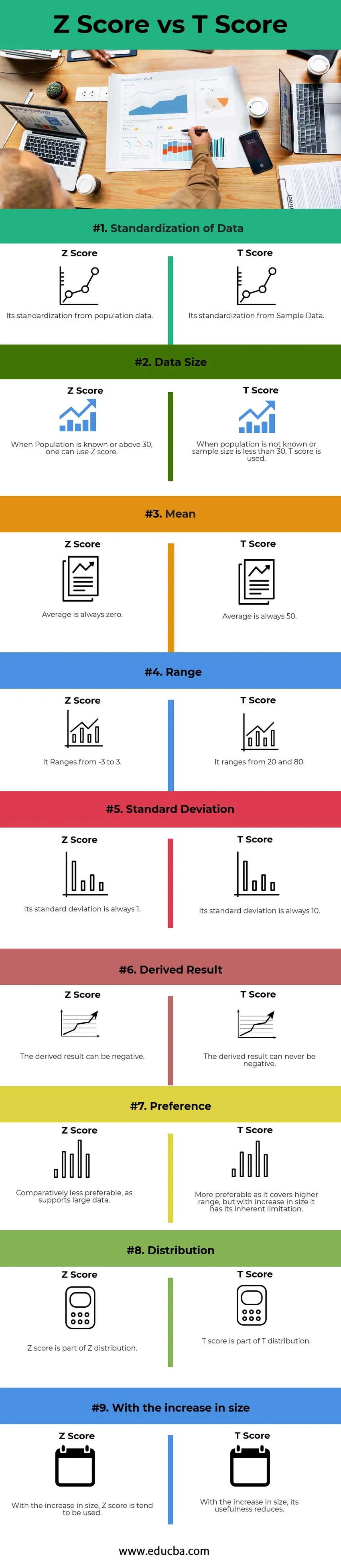
Principais diferenças entre o escore Z e o escore T
Vamos discutir algumas das principais diferenças entre o escore Z vs o escore T
- A pontuação Z é a padronização dos dados brutos da população ou mais de 30 dados da amostra para a pontuação padrão, enquanto a pontuação T é a padronização dos dados da amostra de menos de 30 dados para a pontuação padrão
- O escore Z varia de -3 a 3, enquanto o escore T varia de 20 a 80.
- À medida que o tamanho dos dados aumenta, a distribuição tende a ser a distribuição Z. A distribuição do escore Z versus o escore T faz parte de uma distribuição normal, mas com base no tamanho em que diferem entre si
- Praticamente, o escore Z é amplamente utilizado nos dados do mercado de ações e para verificar as chances de uma empresa entrar em falência, enquanto o escore t é amplamente utilizado na verificação da densidade mineral óssea e nas avaliações de risco à fratura.
Tabela de comparação Z score vs T score
Vejamos o top 9 Comparação entre Z score vs T score
| Sr. Não. | Pontos de comparação | Z Score | Pontuação T |
| 1 | Padronização de dados | Sua padronização a partir de dados populacionais | Sua padronização a partir de dados de amostra |
| 2 | Tamanho dos dados | Quando a população é conhecida ou acima de 30, pode-se usar o escore Z | Quando a população não é conhecida ou o tamanho da amostra é menor que 30, o escore T é usado. |
| 3 | Significar | Uma média é sempre zero. | Uma média é sempre 50. |
| 4 | Alcance | Varia de -3 a 3. | Varia de 20 e 80. |
| 5 | Desvio padrão | Seu desvio padrão é sempre 1 | Seu desvio padrão é sempre 10 |
| 6 | Resultado Derivado | O resultado derivado pode ser negativo | O resultado derivado nunca pode ser negativo |
| 7 | Preferência | Comparativamente menos preferível, pois suporta grandes dados | Mais preferível, pois abrange uma faixa mais alta, mas com um aumento no tamanho, tem sua limitação inerente |
| 8 | Distribuição | A pontuação Z faz parte da distribuição Z | A pontuação T faz parte da distribuição T |
| 9 | Com o aumento do tamanho | Com o aumento do tamanho, o escore Z tende a ser usado | Com o aumento do tamanho, sua utilidade diminui. |
Conclusão
Tanto o escore Z quanto o escore T fazem parte do teste de hipóteses sob a distribuição normal. Se você tiver um conjunto de pontuações de medidas em diferentes medidas usando a pontuação Z, poderá dizer como as pontuações são colocadas em suas distribuições. Então você pode compará-los. A padronização das pontuações é um procedimento amplamente utilizado no campo da pesquisa e do planejamento, pois ajuda na comparação de várias pontuações de testes. Padronizar as pontuações antes de combiná-las ajuda o pesquisador a obter resultados melhores e comparáveis.
Artigos recomendados
Este foi um guia para a principal diferença entre o escore Z vs o escore T. Aqui também discutimos as principais diferenças entre o escore Z e o T com infográficos e tabela de comparação. Você também pode dar uma olhada nos seguintes artigos para saber mais:
- Finanças vs Economia - Diferença
- Déficit vs Dívida - Qual é o Melhor
- Compra de Ativos vs Compra de Ações
- Mercado monetário vs mercado de capitais
- Visão geral do Altman Z Score