
Introdução às funções em R
A função é definida como um conjunto de instruções, para executar e realizar qualquer tarefa lógica específica. A função utiliza alguns parâmetros de entrada conhecidos como argumentos para executar essa tarefa. As funções ajudam a quebrar o código, em partes mais simples, orquestrando-o logicamente, o que é mais fácil de ler e entender. Neste tópico, vamos aprender sobre Funções em R.
Como escrever funções em R?
Para escrever a função em R, aqui está a sintaxe:
Fun_name <- function (argument) (
Function body
)
Aqui, pode-se ver a palavra reservada específica da “função” usada em R, para definir qualquer função. A função recebe entrada que está na forma de argumentos. O corpo da função é um conjunto de instruções lógicas que são executadas sobre argumentos e, em seguida, retorna a saída. "Fun_name" é o nome dado à função, através da qual ela pode ser chamada em qualquer lugar do programa R.
Vamos ver um exemplo, que será mais lúcido na compreensão do conceito de função em R.
Código R
Multi <- function(x, y) (
# function to print x multiply y
result <- x*y
print(paste(x, "Multiply", y, "is", result))
)
resultado:
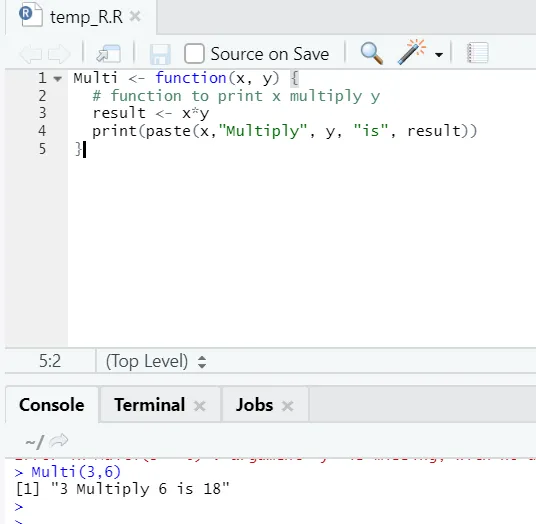
Aqui, criamos o nome da função “Multi”, que recebe dois argumentos como entradas e fornece a saída multiplicada. O primeiro argumento é x e o segundo argumento é y. Como você pode ver, chamamos a função pelo nome "Multi". Aqui, se alguém quiser, os argumentos também poderão ser configurados para o valor padrão.
Diferentes tipos de funções em R
Diferentes funções R com sintaxe e exemplos (interno, matemática, estatística etc.)
1) Função Integrada -
Essas são as funções que acompanham o R para abordar uma tarefa específica, assumindo um argumento como entrada e fornecendo uma saída com base na entrada fornecida. Vamos discutir algumas funções gerais importantes de R aqui:
a) Classificação: os dados podem ser da ordem crescente ou decrescente. Os dados podem ser se um vetor de variável contínua ou variável de fator.
Sintaxe:

Aqui está a explicação de seus parâmetros:
- x: este é um vetor da variável contínua ou variável de fator
- decrescente: pode ser definido como Verdadeiro / Falso para controlar a ordem, subindo ou descendo. Por padrão, é FALSE`.
- last: Se o vetor tiver valores de NA, deve ser colocado por último ou não
Código R e saída:
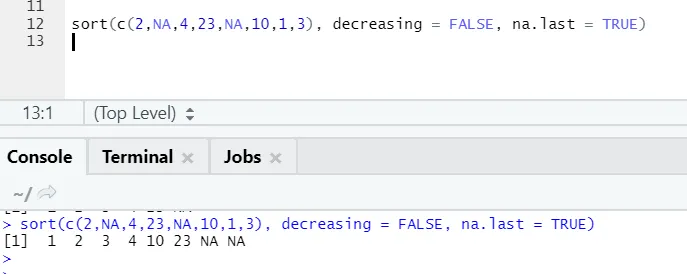
Aqui é possível notar como os valores de “NA” são alinhados no final. Como nosso parâmetro na.last = True era verdadeiro.
b) Seq: gera uma sequência do número entre dois números especificados.
Sintaxe
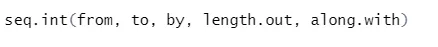
Aqui está a explicação de seus parâmetros:
- de, para o valor inicial e final da sequência.
- por: Incremento / intervalo entre dois números consecutivos em sequência
- length.out: o comprimento necessário da sequência.
- Along.with: refere-se ao comprimento do comprimento deste argumento
Código R e saída:
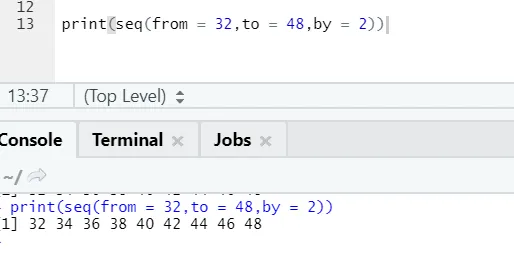
Aqui pode-se notar que a sequência gerada está tendo um incremento de 2 porque by é definido como 2.
c) Toupper, tolower: As duas funções: toupper e tolower são funções aplicadas na string para alterar os casos das letras nas frases.
Código R e saída:
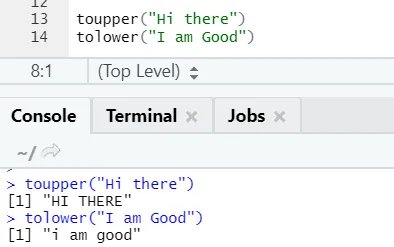
Pode-se notar como os casos de letras são alterados quando aplicados à função.
d) Rnorm: Esta é uma função interna que gera números aleatórios.
Código R e saída:
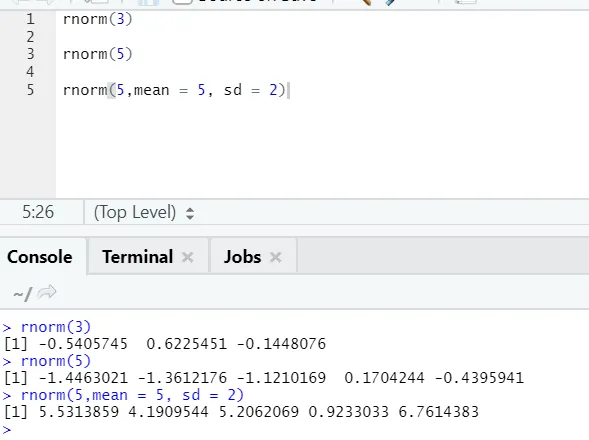
A função rnorm pega o primeiro argumento que diz quantos números precisam ser gerados.
e) Rep: Esta função replica o valor quantas vezes for especificado.
Sintaxe de R: rnorm (x, n)
Aqui x representa o valor a ser replicado en representa o número de vezes que ele precisa ser replicado.
Código R e saída:
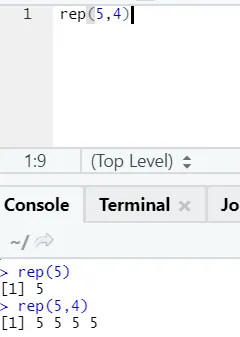
f) Colar: Esta função é concatenar seqüências de caracteres juntamente com algum caractere específico no meio.
sintaxe
paste(x, sep = “”, collapse = NULL)
Código R
paste("fish", "water", sep=" - ")
Saída R:
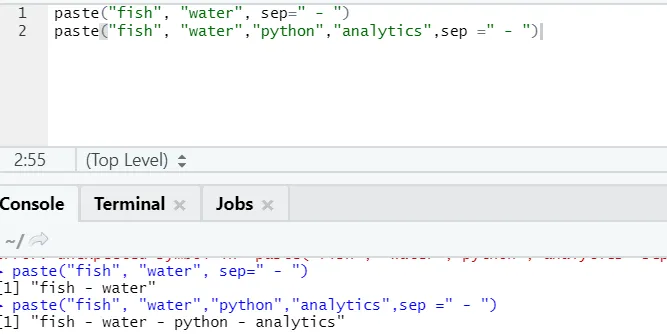
Como você pode ver, também podemos colar mais de duas strings. Sep é o caractere específico que adicionamos entre as strings. Por padrão, sep é espaço.
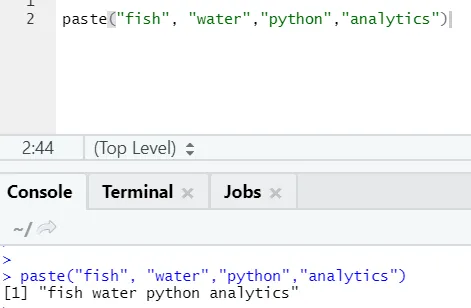
Existe mais uma função semelhante como esta, da qual todos devem estar atentos é paste0.
A função paste0 (x, y, recolhimento) funciona de maneira semelhante à pasta (x, y, sep = “”, recolhimento)
Por favor, veja o exemplo abaixo:
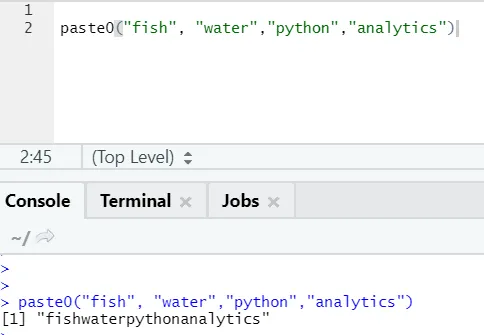
Em palavras simples, para resumir colar e colar 0:
Colar0 é mais rápido que colar quando se trata da concatenação de seqüências de caracteres sem nenhum separador. Como colar, sempre procure "sep" e, por padrão, é o espaço.
g) Strsplit: Esta função é dividir a string. Vamos ver os casos simples:
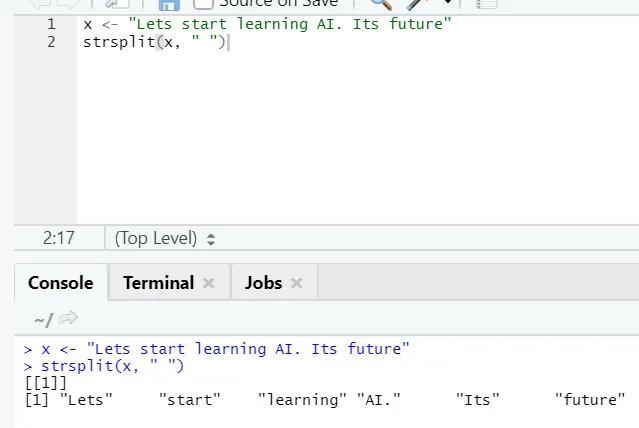
h) Rbind: A função rbind ajuda a pentear vetores com o mesmo número de colunas, uma sobre a outra.
Exemplo
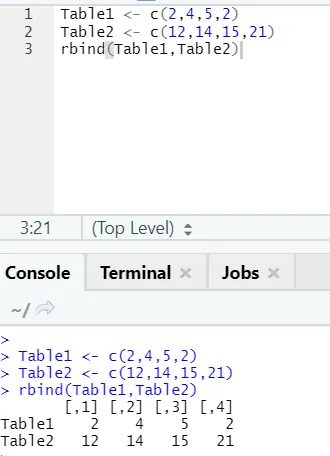
i) cbind: combina vetores com o mesmo número de linhas, lado a lado.
Exemplo
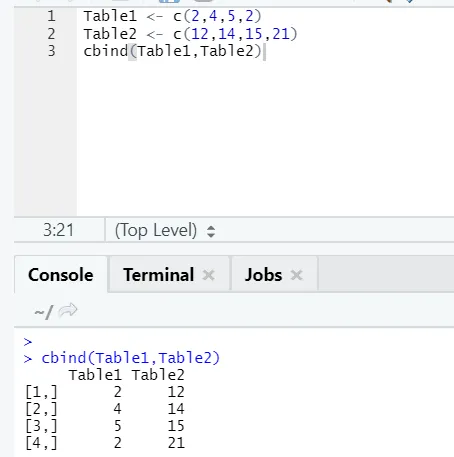
Caso o número de linhas não corresponda, abaixo está o erro que você encontrará:

O cbind e o rbind ajudam na manipulação e remodelagem de dados.
2) Função Matemática -
R fornece uma ampla variedade de funções matemáticas. Vamos ver alguns deles em detalhes:
a) Sqrt: Esta função calcula a raiz quadrada de um número ou vetor numérico.
Código R e saída:
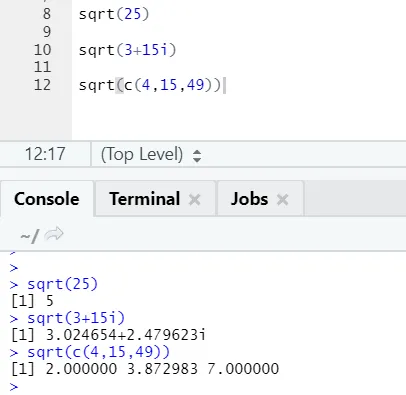
Pode-se ver como a raiz quadrada de um número, número complexo e uma sequência de vetores numéricos foram calculados.
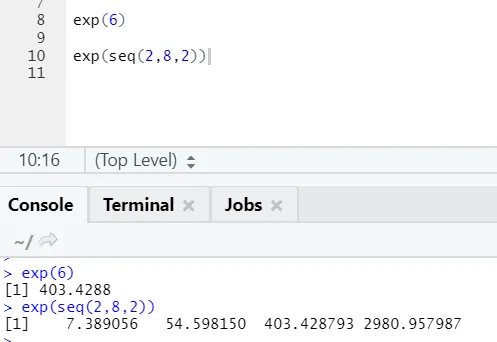
b) Exp: Esta função calcula o valor exponencial de um número ou um vetor numérico.
Código R e saída:
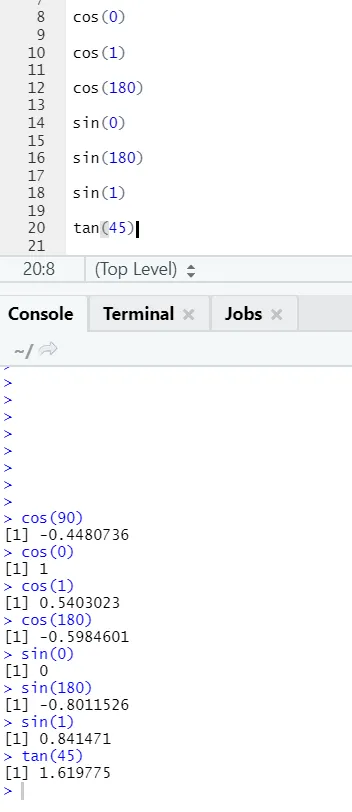
c) Cos, Sin, Tan: Estas são funções trigonométricas implementadas em R aqui.
Código R e saída:
d) Abs: Esta função retorna o valor positivo absoluto de um número.
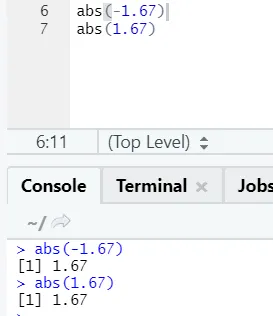
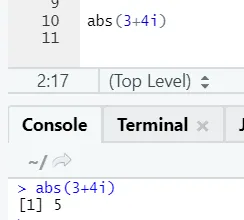
Como você pode ver, o negativo ou positivo de um número será retornado em sua forma absoluta. Vamos ver um número complexo:
e) Log: Este é o logaritmo de um número.
Aqui está o exemplo é mostrado abaixo:
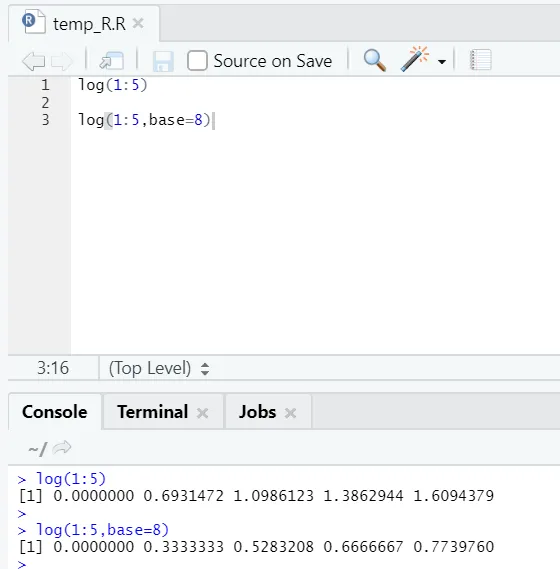
Aqui se obtém a flexibilidade de alterar a base, conforme o requisito.
f) Cumsum: Esta é uma função matemática que fornece somas cumulativas. Aqui está o exemplo abaixo:
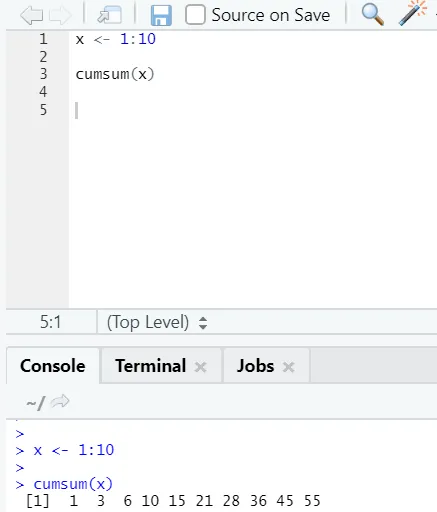
g) Cumprod: como a função matemática Cumsum, temos cumprod onde a multiplicação cumulativa acontece.
Por favor, veja o exemplo abaixo:
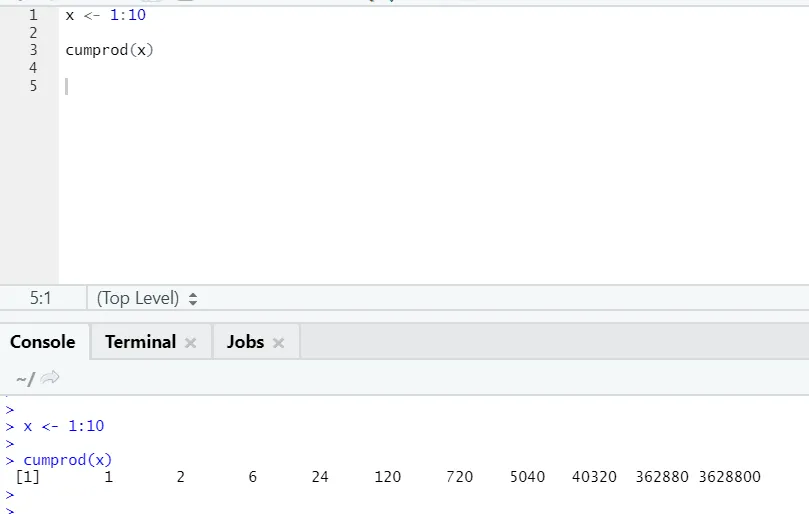
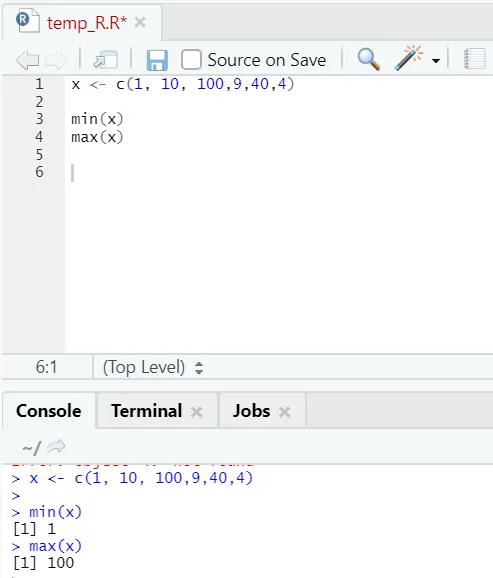
h) Max, Min: Isso ajudará você a encontrar o valor máximo / mínimo no conjunto de números. Veja abaixo os exemplos relacionados a isso:
i) Teto: O teto é uma função matemática que retorna o menor número inteiro maior que o especificado.
Vamos ver um exemplo:
teto (2, 67)
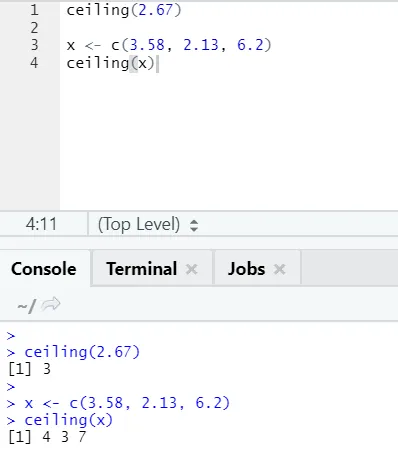
Como você pode notar, o teto é aplicado sobre um número e também sobre uma lista, e a saída obtida é o menor do próximo número inteiro mais alto.
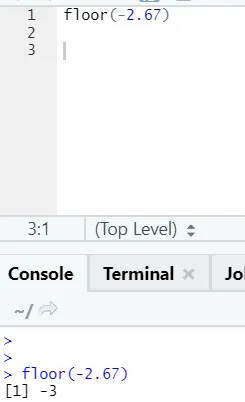
j) Piso: o piso é uma função matemática que retorna o menor valor inteiro do número especificado.
O exemplo mostrado abaixo ajudará você a entender melhor:
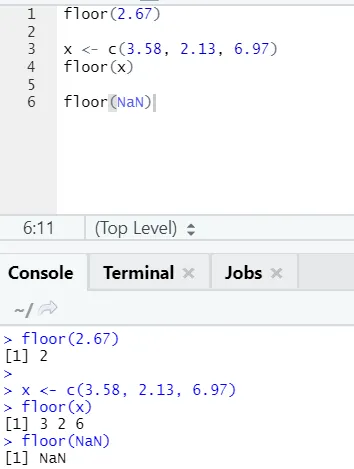
Funciona da mesma maneira para valores negativos também. Por favor dê uma olhada:
3) Funções estatísticas -
Essas são as funções que descrevem a distribuição de probabilidade relacionada.
a) Mediana: Calculou a mediana a partir da sequência de números.
Sintaxe
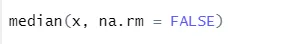
Código R e saída:
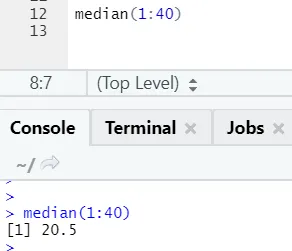
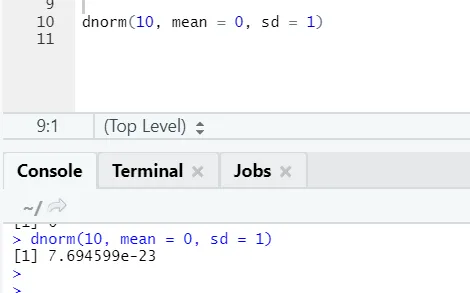
b) Dnorm: Refere-se à distribuição normal. A função dnorm retorna o valor da função densidade de probabilidade, para a distribuição normal dados os parâmetros para x, μ e σ.
Código R e saída:
c) Cov: Covariância diz se dois vetores são positivos, negativos ou totalmente não relacionados.
Código R
x_new = c(1., 5.5, 7.8, 4.2, -2.7, -5.5, 8.9)
y_new = c(0.1, 2.0, 0.8, -4.2, 2.7, -9.4, -1.9)
cov(x_new, y_new)
Saída R:
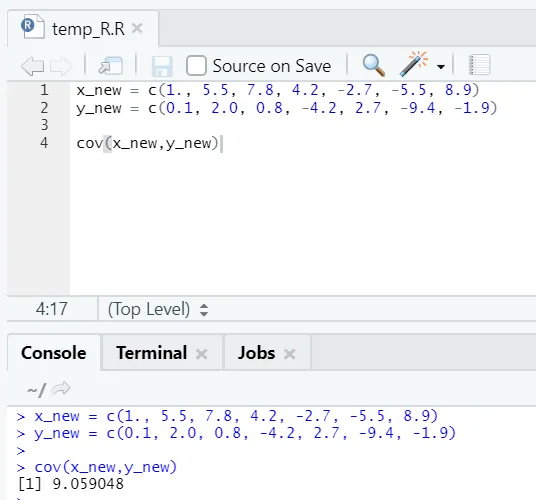
Como você pode ver, dois vetores estão positivamente relacionados, o que significa que ambos os vetores se movem na mesma direção. Se a covariância é negativa, significa que x e y estão inversamente relacionados e, portanto, se movem na direção oposta.
d) Cor: Esta é uma função para encontrar a correlação entre vetores. Na verdade, fornece o fator de associação entre os dois vetores, conhecido como "coeficiente de correlação". A correlação adiciona um fator de grau à covariância. Se dois vetores estiverem correlacionados positivamente, a correlação também informará com que extensão eles estão relacionados positivamente.
Esses três tipos de métodos que podem ser usados para encontrar uma correlação entre dois vetores:
- Correlação de Pearson
- Correlação de Kendall
- Correlação de Spearman
No formato R simples, ele se parece com:
cor(x, y, method = c("pearson", "kendall", "spearman"))
Aqui x e y são vetores.
Vamos ver o exemplo prático de correlação sobre um conjunto de dados embutido.
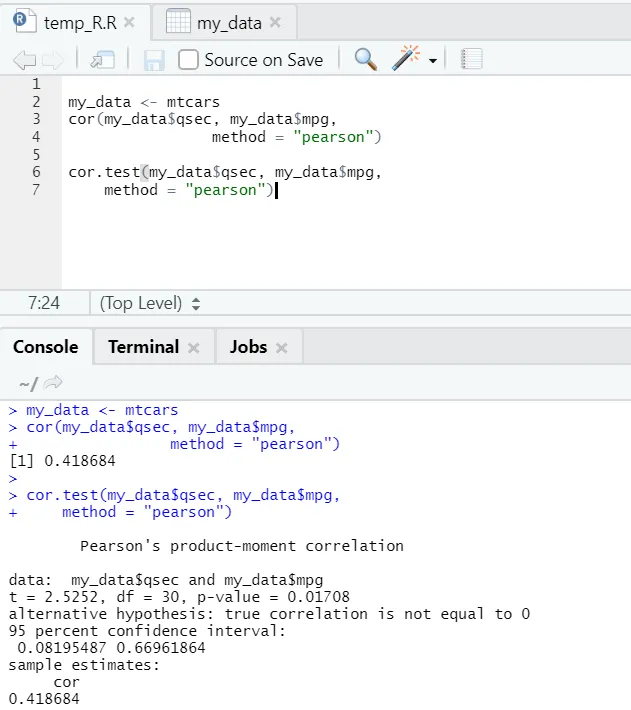
Então, aqui você pode ver a função "cor ()" que deu o coeficiente de correlação 0, 41 entre "qsec" e "mpg". No entanto, mais uma função também foi exibida, ou seja, “cor.test ()”, que não apenas informa o coeficiente de correlação, mas também o valor p et valor relacionado a ela. A interpretação se torna muito mais fácil com a função cor.test.
Semelhante pode ser feito com os outros dois métodos de correlação:
Código R para o método Pearson:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = " pearson ")
cor.test(my_data$qsec, my_data$mpg, method = " pearson")
Código R para o método Kendall:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = " kendall")
cor.test(my_data$qsec, my_data$mpg, method = " kendall")
Código R para o método Spearman:
my_data <- mtcars
cor(my_data$qsec, my_data$mpg, method = "spearman")
cor.test(my_data$qsec, my_data$mpg, method = "spearman")
O coeficiente de correlação varia entre -1 e 1.
Se o coeficiente de correlação for negativo, isso implica quando x aumenta y diminui.
Se o coeficiente de correlação for zero, isso implica que não existe associação entre x e y.
Se o coeficiente de correlação for positivo, isso implica que x aumenta y também tende a aumentar.
e) Teste T: O teste T informará se dois conjuntos de dados são provenientes das mesmas (supondo) distribuições normais ou não.
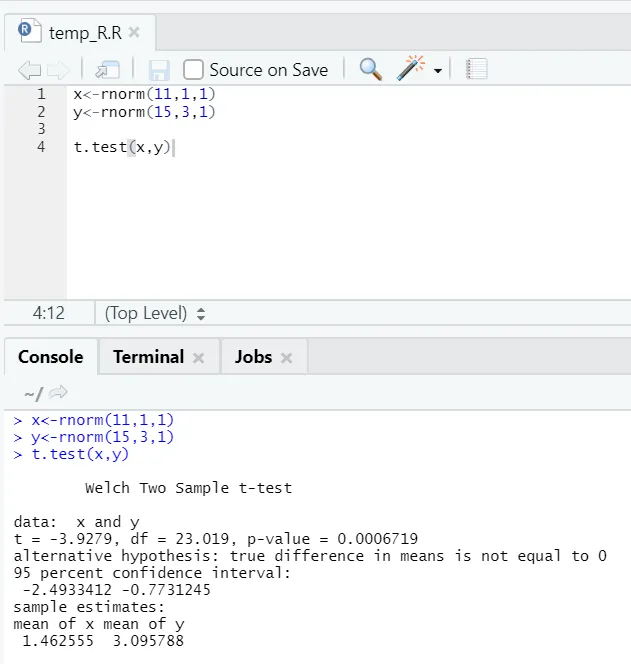
Aqui você deve rejeitar a hipótese nula de que as duas médias são iguais porque o valor de p é menor que 0, 05.
A instância mostrada é do tipo: conjuntos de dados não emparelhados com variações desiguais. Da mesma forma, pode ser tentado com o conjunto de dados emparelhado.
f) Regressão linear simples: mostra a relação entre a variável preditora / independente e resposta / dependente.
Um exemplo prático simples pode ser a previsão do peso de uma pessoa, se a altura for conhecida.
Sintaxe R
lm(formula, data)
Aqui, a fórmula descreve a relação entre a saída ie ie a variável de entrada iex Os dados representam o conjunto de dados, no qual a fórmula precisa ser aplicada.
Vamos ver um exemplo prático, onde a área do piso é a variável de entrada e aluguel é a variável de saída.
x <- c (1510, 1000, 600, 500, 1280, 136, 1790, 1630)
y <- c (15000, 10000, 6000, 5000, 12800, 13600, 17900, 16300)
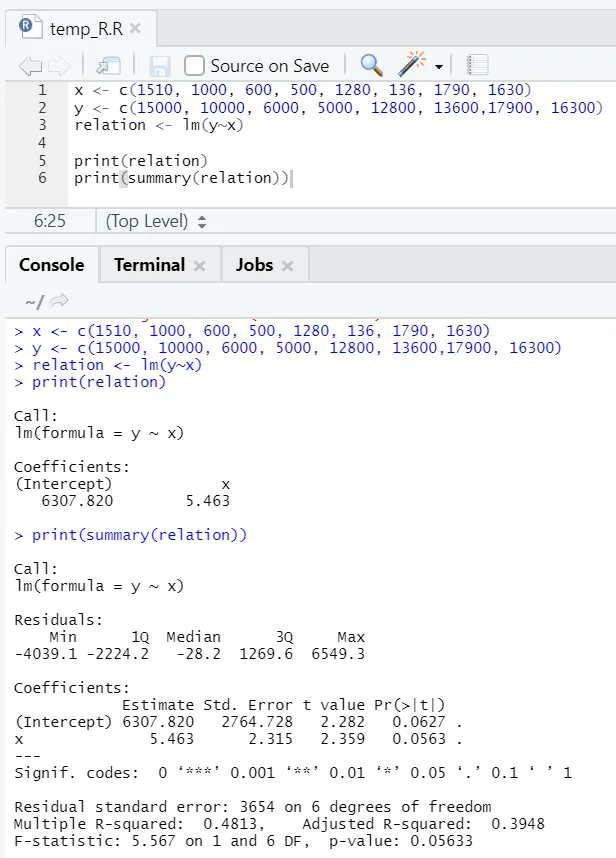
Aqui o valor P não é inferior a 5%. Portanto, a hipótese nula não pode ser rejeitada. Não há muito significado para provar a relação entre a área útil e o aluguel.
Aqui o valor do quadrado R é 0, 4813. Isso implica que apenas 48% da variação na variável de saída pode ser explicada pela variável de entrada.
Digamos que agora precisamos prever um valor da área do piso, com base no modelo acima ajustado.
Código R
x_new <- data.frame(x = 1700)
result <- predict(relation, x_new)
print(result)
Saída R:
Após a execução do código R acima, a saída será semelhante à seguinte:
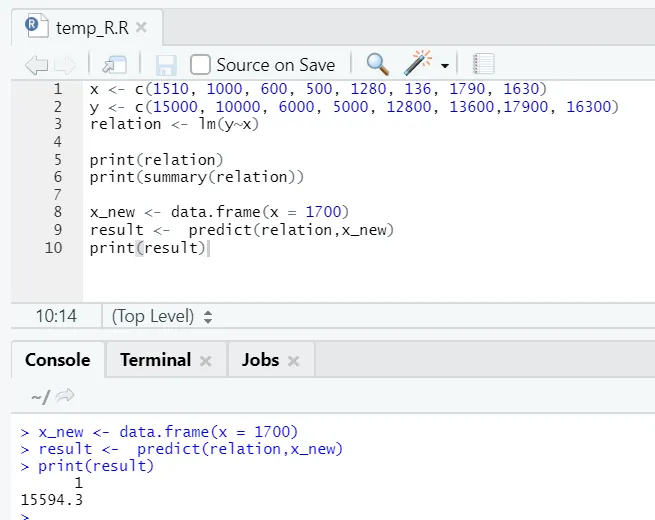
Pode-se ajustar e visualizar a regressão. Aqui está o código R para isso:
# Dê um nome ao arquivo do gráfico png.
png(file = "LinearRegressionSample.png.webp")
# Traçar o gráfico.
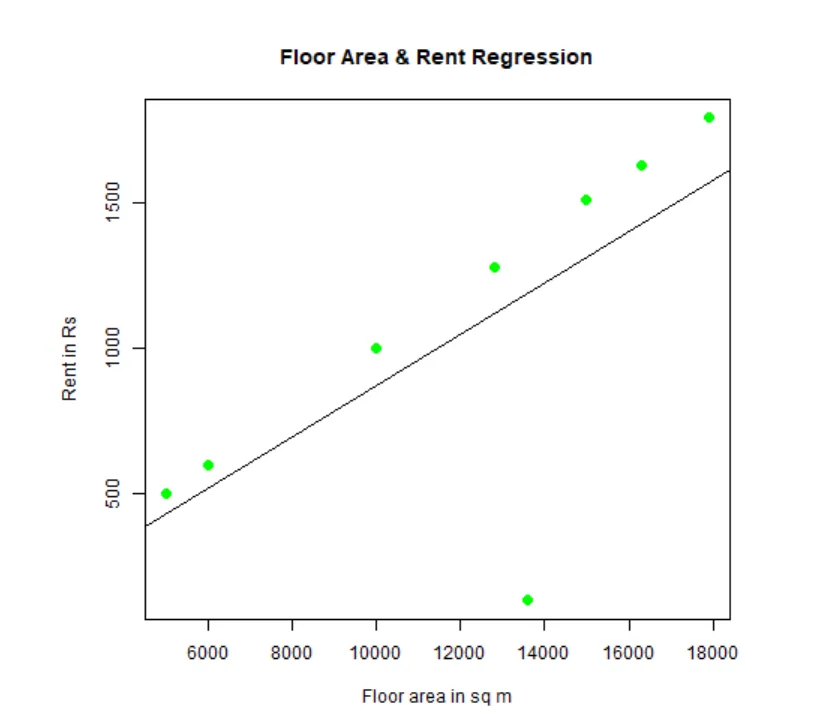
plot(y, x, col = "green", main = "Floor Area & Rent Regression",
abline(lm(x~y)), cex = 1.3, pch = 16, xlab = "Floor area in sq m", ylab = "Rent in Rs")
# Salve o arquivo.
dev.off()
Este gráfico “LinearRegressionSample.png.webp” será gerado no seu diretório de trabalho atual.
g) Teste do qui-quadrado
Esta é uma função estatística em R. Este teste mantém seu significado para provar se existe correlação entre duas variáveis categóricas.
Este teste também funciona como qualquer outro teste estatístico baseado no valor-p; pode-se aceitar ou rejeitar a hipótese nula.
Sintaxe R
chisq.test(data), /code>
Vamos ver um exemplo prático disso.
Código R
# Carrega a biblioteca.
library(datasets)
data(iris)
# Crie um quadro de dados a partir do conjunto de dados principal.
iris.data <- data.frame(iris$Sepal.Length, iris$Sepal.Width)
# Crie uma tabela com as variáveis necessárias.
iris.data = table(iris$Sepal.Length, iris$Sepal.Width)
print(iris.data)
# Realize o teste do qui-quadrado.
print(chisq.test(iris.data))
Saída R:
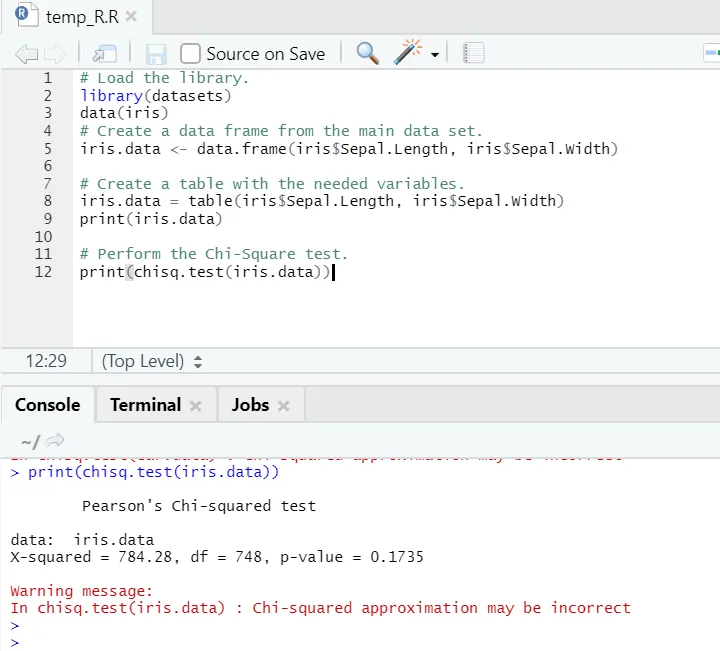
Como se pode ver, o teste do qui-quadrado foi realizado em um conjunto de dados da íris, considerando suas duas variáveis “Sepal. Length ”e“ Sepal.Width ”.
O valor de p não é menor que 0, 05, portanto, não existe correlação entre essas duas variáveis. Ou podemos dizer que essas duas variáveis não dependem uma da outra.
Conclusão
As funções em R são simples, fáceis de ajustar, fáceis de entender e, no entanto, muito poderosas. Vimos uma variedade de funções que são usadas como parte do básico em R. Quando alguém se familiariza com essas funções discutidas acima, pode-se explorar outras variedades de funções. As funções ajudam você a executar seu código de maneira simples e concisa. As funções podem ser incorporadas ou definidas pelo usuário, tudo depende da necessidade de resolver um problema. As funções dão uma boa forma a um programa.
Artigos recomendados
Este é um guia para Funções em R. aqui discutimos como escrever Funções em R e diferentes tipos de Funções em R com sintaxe e exemplos. Você também pode consultar o seguinte artigo para saber mais -
- Funções de String R
- Funções de seqüência de caracteres SQL
- Funções de seqüência de caracteres T-SQL
- Funções de string do PostgreSQL