
Fórmula do coeficiente de variação (Sumário)
- Fórmula
- Exemplos
Qual é a fórmula do coeficiente de variação?
Nas estatísticas, o coeficiente de variação também denominado CV é uma ferramenta que nos ajuda a determinar como os pontos de dados em um conjunto de dados são distribuídos pela média. Basicamente, todos os pontos de dados são plotados primeiro e, em seguida, o coeficiente de variação é usado para medir a dispersão desses pontos um do outro e a média. Isso nos ajuda a entender os dados e também a ver o padrão que eles formam. É calculado como uma razão do desvio padrão do conjunto de dados para o valor médio. Maior o coeficiente de variação significa que há um nível maior de dispersão dos dados em torno da média. Da mesma forma, quanto menor o valor do coeficiente de variação, menor a dispersão e mais precisos serão os resultados. Mesmo que a média de duas séries de dados seja consideravelmente diferente, o coeficiente de variação é muito útil para comparar o grau de variação de uma série de dados para outra.
A fórmula do coeficiente de variação é dada por:
Coefficient of Variation = Standard Deviation / Mean
Etapas para calcular o coeficiente de variação:
Etapa 1: calcule a média do conjunto de dados. Média é a média de todos os valores e pode ser calculada pegando a soma de todos os valores e dividindo-a por um número de pontos de dados.
Etapa 2: depois calcule o desvio padrão do conjunto de dados. Esse é um processo demorado. O desvio padrão pode ser calculado como: √ (Σ (X i - X m ) 2 / (n - 1)) . X i é o i-ésimo ponto de dados e X m é a média do conjunto de dados. Como alternativa, também podemos encontrar o desvio padrão no excel usando a função DESVPAD.S ().
Etapa 3: Divida o desvio padrão por média para obter o coeficiente de variação.
Exemplos de fórmula de coeficiente de variação (com modelo do Excel)
Vamos dar um exemplo para entender melhor o cálculo do coeficiente de variação.
Você pode fazer o download deste modelo do Excel com coeficiente de variação aqui - Modelo do Excel com coeficiente de variaçãoFórmula do coeficiente de variação - Exemplo # 1
Digamos que temos dois conjuntos de dados A e B e cada um contém 20 pontos de dados aleatórios. Calcule o coeficiente de variação para o conjunto de dados X e Y.
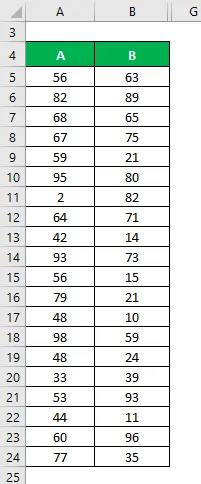
Solução:
A média é calculada como:
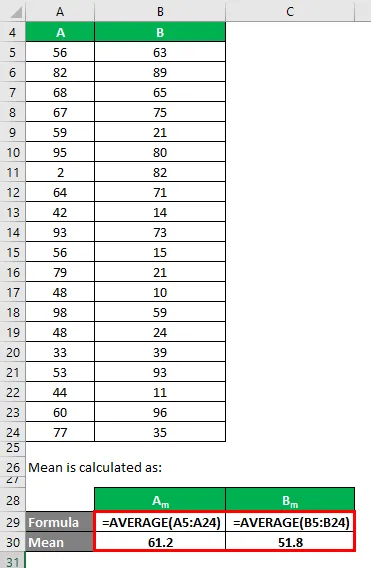
- Média do conjunto de dados A = 61, 2
- Média do conjunto de dados B = 51, 8
Agora, precisamos calcular a diferença entre os pontos de dados e o valor médio.
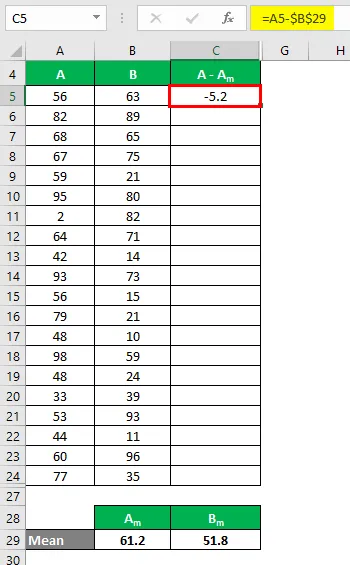
Da mesma forma, calcule para todos os valores do conjunto de dados A.
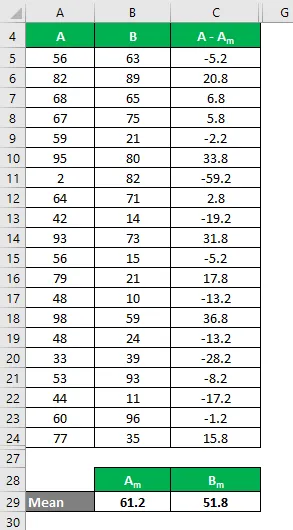
Da mesma forma, calcule para todos os valores do conjunto de dados B.
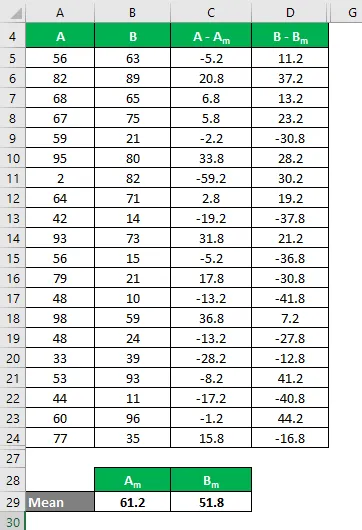
Calcule o quadrado da diferença para os conjuntos de dados A e B.
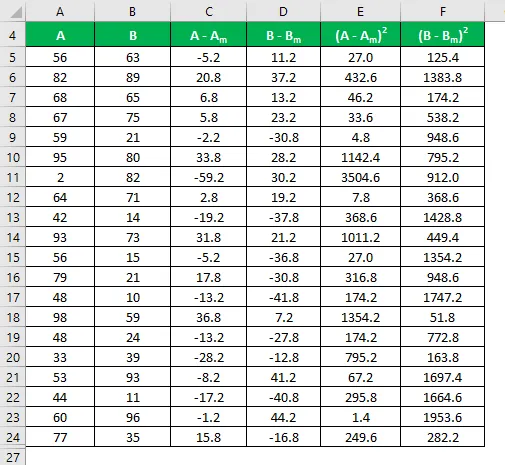
O desvio padrão é calculado usando a fórmula abaixo
Desvio padrão = √ (Σ (X i - X m ) 2 / (n - 1))
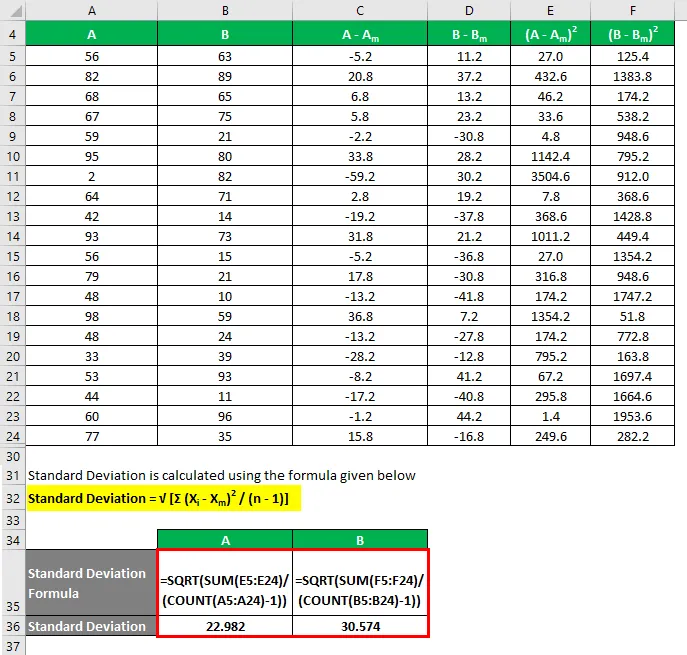
O coeficiente de variação é calculado usando a fórmula abaixo
Coeficiente de variação = desvio padrão / média
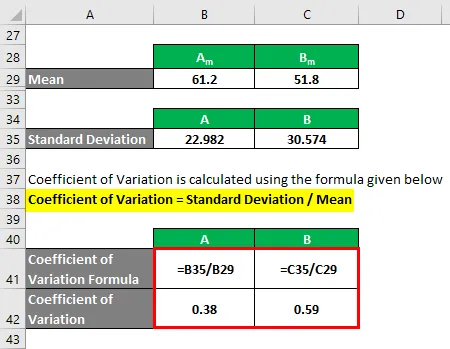
- Coeficiente de variação A = 22.982 / 61, 2 = 0, 38
- Coeficiente de variação B = 30.574 / 51, 8 = 0, 59
Portanto, se você vê aqui, B tem um coeficiente de variação maior que A, o que significa que os pontos de dados de B são mais dispersos que A.
Fórmula do Coeficiente de Variação - Exemplo # 2
Digamos que você seja um investidor muito avesso ao risco e deseja investir dinheiro no mercado de ações. Como seu apetite ao risco é baixo, você deseja investir em ações seguras com menor desvio padrão e coeficiente de variação. Você selecionou 3 ações com base em suas informações técnicas e fundamentais e deseja escolher 2 ações. Você também coletou informações sobre seus retornos históricos nos últimos 15 anos.
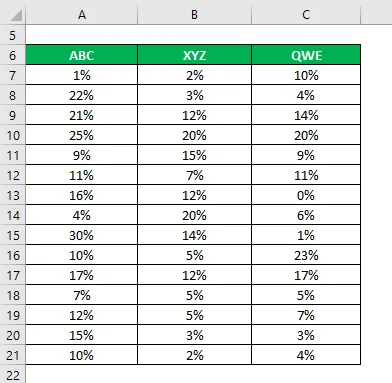
Solução:
A média é calculada como:
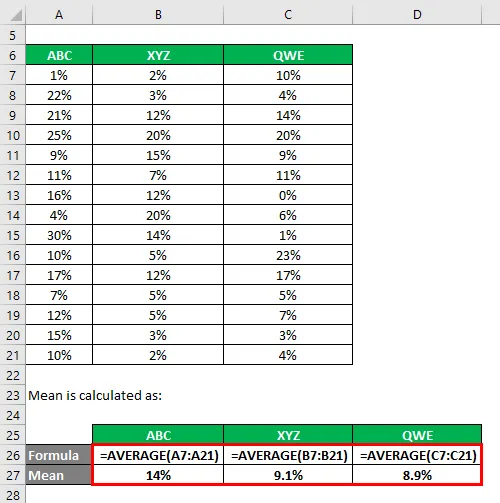
O desvio padrão é calculado usando a fórmula do excel
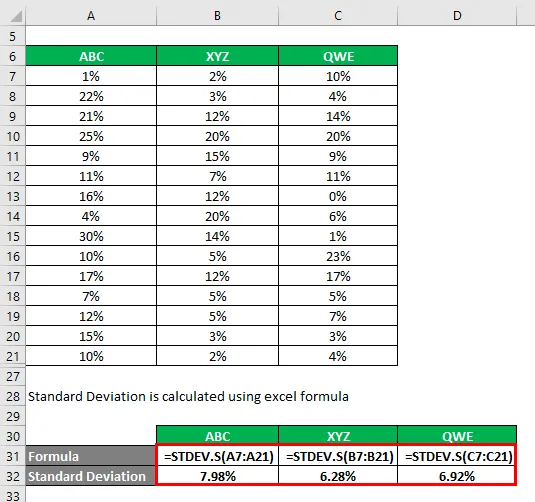
O coeficiente de variação é calculado usando a fórmula abaixo
Coeficiente de variação = desvio padrão / média
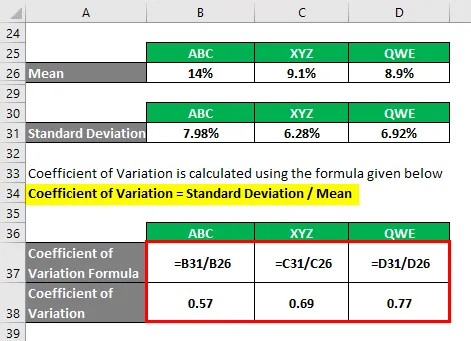
- Coeficiente de variação ABC = 7, 98% / 14% = 0, 57
- Coeficiente de variação XYZ = 6, 28% / 9, 1% = 0, 69
- Coeficiente de Variação QWE = 6, 92% / 8, 9% = 0, 77
Com base nas informações, você escolherá as ações ABC e XYZ para investir, pois elas têm o menor coeficiente de variação.
Explicação
Como o coeficiente de variação é uma medida de risco, ajuda a medir a volatilidade nos preços das ações e outros instrumentos financeiros. Também ajuda investidores e analistas a comparar os riscos associados a diferentes investimentos potenciais.
O coeficiente de variação é semelhante ao desvio padrão, mas um desvio padrão de duas variáveis não pode ser comparado em útil. Mas usar o desvio padrão e a média torna a comparação relativa mais significativa. Há uma limitação do coeficiente de variação também. Suponha que a média de um conjunto de dados seja zero. Nesse caso, essa ferramenta se tornará ineficaz. Além disso, se tivermos um conjunto de dados com muitos valores positivos e negativos, o coeficiente de variação se torna muito problemático. Portanto, é apenas mais útil com conjuntos de dados com o mesmo sinal de mais-menos.
Relevância e usos da fórmula do coeficiente de variação
O coeficiente de variação tem relevância em muitos outros campos além das estatísticas. Por exemplo, no campo das finanças, o coeficiente de variação é uma medida de risco. É semelhante ao desvio padrão, uma vez que também é usado como uma medida de risco, mas a diferença é que o coeficiente de variação é um melhor indicador de risco relativo. Por exemplo, digamos que o retorno esperado de A de 15% e o retorno esperado de B de 10% e A tenha um desvio padrão de 10%, enquanto B tenha um desvio padrão de 5%. Para escolher um investimento melhor, o coeficiente de variação pode ser usado. Portanto, o coeficiente de variação de A é 10/15 = 0, 666 e o coeficiente de variação de B é 5/10 = 0, 5. Então B é um investimento melhor que A.
Artigos recomendados
Este foi um guia para a fórmula do coeficiente de variação. Aqui discutimos como calcular o coeficiente de variação usando a fórmula, juntamente com exemplos práticos e modelo de excel para download. Você também pode consultar os seguintes artigos para saber mais -
- O que é a fórmula ao quadrado R ajustada?
- Exemplos de fórmula do coeficiente de determinação
- Como calcular o coeficiente de correlação usando a fórmula?
- Modelo de fórmula de covariância com Excel