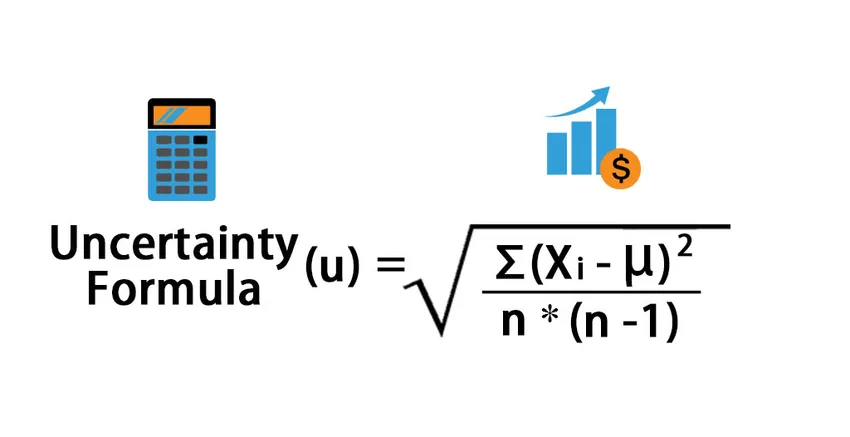
Fórmula de incerteza (Sumário)
- Fórmula
- Exemplos
O que é a Fórmula da Incerteza?
Na linguagem estatística, o termo “incerteza” está associado a uma medida em que se refere à variação esperada do valor, derivada de uma média de várias leituras, da média real do conjunto de dados ou leituras. Em outras palavras, a incerteza pode ser considerada como o desvio padrão da média do conjunto de dados. A fórmula para a incerteza pode ser derivada somando os quadrados do desvio de cada variável da média, depois divida o resultado pelo produto do número de leituras e o número de leituras menos um e depois calcule a raiz quadrada do resultado . Matematicamente, a Fórmula da Incerteza é representada como,
Uncertainty (u) = √ (∑ (x i – μ) 2 / (n * (n – 1)))
Onde,
- x i = iésima leitura no conjunto de dados
- μ = Média do conjunto de dados
- n = Número de leituras no conjunto de dados
Exemplos de fórmula de incerteza (com modelo do Excel)
Vamos dar um exemplo para entender melhor o cálculo da incerteza.
Você pode fazer o download deste modelo de fórmula de incerteza do Excel aqui - Modelo de fórmula de incerteza do ExcelFórmula de Incerteza - Exemplo # 1
Vamos dar o exemplo de uma corrida de 100m em um evento escolar. A corrida foi cronometrada usando cinco cronômetros diferentes e cada cronômetro registrou um tempo ligeiramente diferente. As leituras são 15, 33 segundos, 15, 21 segundos, 15, 31 segundos, 15, 25 segundos e 15, 35 segundos. Calcule a incerteza do tempo com base nas informações fornecidas e apresente o tempo com um nível de confiança de 68%.
Solução:
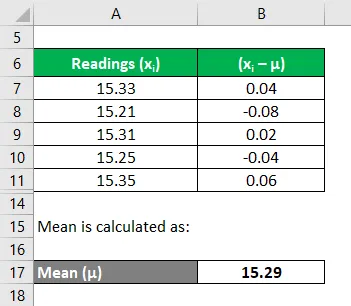
A média é calculada como:
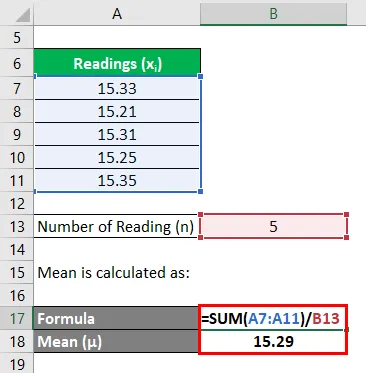
Agora, precisamos calcular os desvios de cada leitura
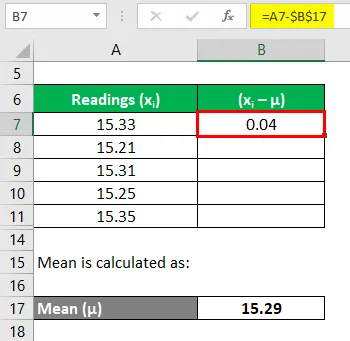
Da mesma forma, calcule para todas as leituras
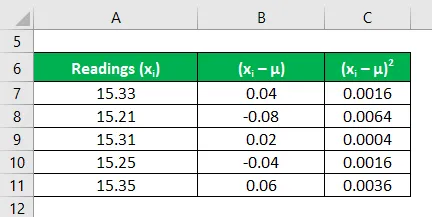
Calcular o quadrado dos desvios de cada leitura
A incerteza é calculada usando a fórmula abaixo
Incerteza (u) = √ (∑ (x i - μ) 2 / (n * (n-1)))
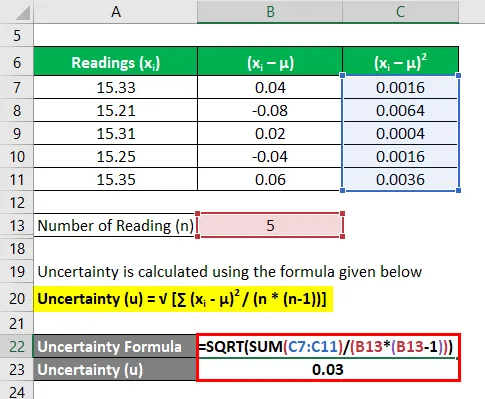
- Incerteza = 0, 03 segundos
Tempo no nível de confiança de 68% = μ ± 1 * u
- Medição com nível de confiança de 68% = (15, 29 ± 1 * 0, 03) segundos
- Medição com nível de confiança de 68% = (15, 29 ± 0, 03) segundos
Portanto, a incerteza do conjunto de dados é de 0, 03 segundos e o tempo pode ser representado como (15, 29 ± 0, 03) segundos no nível de confiança de 68%.
Fórmula de Incerteza - Exemplo # 2
Tomemos o exemplo de João, que decidiu vender sua propriedade imobiliária, que é uma terra árida. Ele quer medir a área disponível da propriedade. De acordo com o inspetor designado, foram realizadas 5 leituras - 50, 33 acres, 50, 20 acres, 50, 51 acres, 50, 66 acres e 50, 40 acres. Expresse a medição da terra com nível de confiança de 95% e 99%.
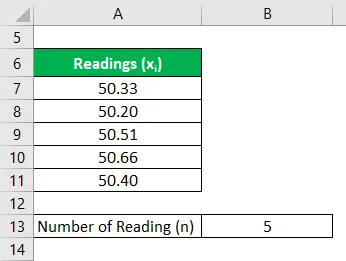
Solução:
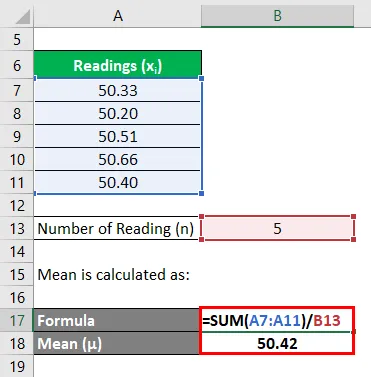
A média é calculada como:
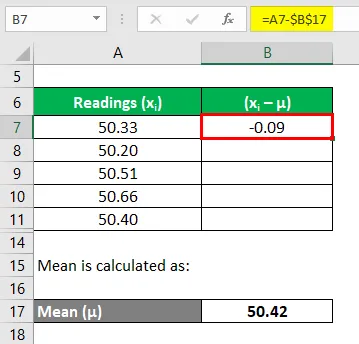
Agora, precisamos calcular os desvios de cada leitura
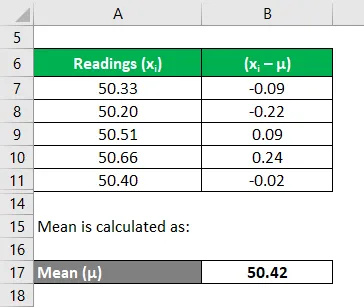
Da mesma forma, calcule para todas as leituras
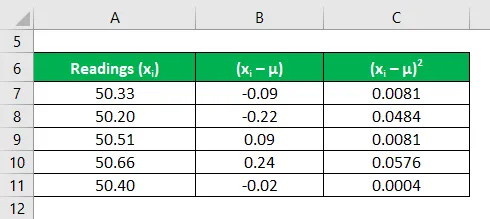
Calcular o quadrado dos desvios de cada leitura
A incerteza é calculada usando a fórmula abaixo
Incerteza (u) = √ (∑ (x i - μ) 2 / (n * (n-1)))
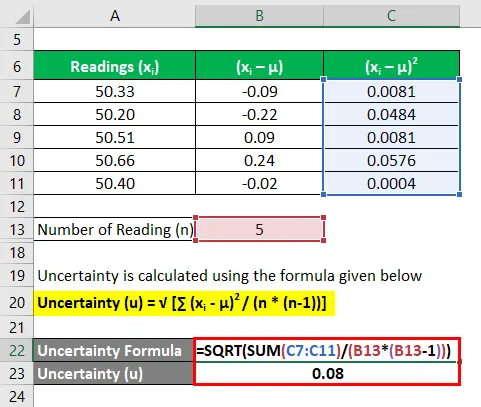
- Incerteza = 0, 08 acres
Medição com nível de confiança de 95% = μ ± 2 * u
- Medição com nível de confiança de 95% = (50, 42 ± 2 * 0, 08) acre
- Medição com nível de confiança de 95% = (50, 42 ± 0, 16) acre
Medição com nível de confiança de 99% = μ ± 3 * u
- Medição com nível de confiança de 99% = (50, 42 ± 3 * 0, 08) acre
- Medição com nível de confiança de 99% = (50, 42 ± 0, 24) acre
Portanto, a incerteza das leituras é de 0, 08 acres e a medição pode ser representada como (50, 42 ± 0, 16) acres e (50, 42 ± 0, 24) acres com nível de confiança de 95% e 99%.
Explicação
A fórmula para a incerteza pode ser derivada usando as seguintes etapas:
Etapa 1: primeiro, selecione o experimento e a variável a ser medida.
Etapa 2: Em seguida, colete um número suficiente de leituras para o experimento através de medições repetidas. As leituras formarão o conjunto de dados e cada leitura será indicada por x i .
Etapa 3: em seguida, determine o número de leituras no conjunto de dados, indicado por n.
Etapa 4: Em seguida, calcule a média das leituras resumindo todas as leituras no conjunto de dados e divida o resultado pelo número de leituras disponíveis no conjunto de dados. A média é denotada por μ.
μ = ∑ x i / n
Etapa 5: Em seguida, calcule o desvio de todas as leituras no conjunto de dados, que é a diferença entre cada leitura e a média, ou seja (x i - μ) .
Etapa 6: Em seguida, calcule o quadrado de todos os desvios, ou seja, (x i - μ) 2 .
Etapa 7: Em seguida, some todos os desvios ao quadrado, ou seja, ∑ (x i - μ) 2 .
Etapa 8: Em seguida, a soma acima é dividida pelo produto de um número de leituras e número de leituras menos um, isto é, n * (n - 1) .
Etapa 9: Finalmente, a fórmula da incerteza pode ser derivada calculando a raiz quadrada do resultado acima, como mostrado abaixo.
Incerteza (u) = √ (∑ (x i - μ) 2 ) / (n * (n-1))
Relevância e usos da fórmula da incerteza
Do ponto de vista dos experimentos estatísticos, o conceito de incerteza é muito importante, pois ajuda um estatístico a determinar a variabilidade nas leituras e estimar a medição com um certo nível de confiança. No entanto, a precisão da incerteza é tão boa quanto as leituras realizadas pelo medidor. A incerteza ajuda a estimar a melhor aproximação para uma medição.
Artigos recomendados
Este foi um guia para a Fórmula da Incerteza. Aqui discutimos como calcular a incerteza usando a fórmula, juntamente com exemplos práticos e modelo de excel para download. Você também pode consultar os seguintes artigos para saber mais -
- Exemplos para calcular o valor absoluto
- Calculadora para a margem da fórmula de erro
- Como calcular o fator de valor presente usando a fórmula?
- Guia para a fórmula relativa de redução de risco