
Fórmula de desvio padrão de amostra (sumário)
- Fórmula
- Exemplos
Fórmula de desvio padrão de amostra
Nas estatísticas, o desvio padrão é basicamente uma medida para encontrar a dispersão dos valores do conjunto de dados do valor médio do conjunto de dados. Ele mede a distância desse ponto de dados e a média. Quanto maior o desvio padrão, maior será a dispersão e os pontos de dados tenderão a ficar longe da média. Da mesma forma, um desvio padrão mais baixo significa que os pontos de dados estarão mais próximos da média. É muito útil na comparação de conjuntos de dados que podem ter o mesmo valor médio, mas um intervalo diferente.
Geralmente, calcule o desvio padrão dos dados da população, mas às vezes os dados da população são tão grandes que não é possível encontrar o desvio padrão para isso. Nesse caso, o desvio padrão da amostra é calculado e isso se tornará o representante do desvio padrão da população. Portanto, assumiremos que a amostra é a representação correta da população e focaremos no desvio padrão da amostra neste artigo.
Suponha que você tenha um conjunto de dados X com pontos de dados (X1, X2 …… ..Xn).
A fórmula para o desvio padrão da população é dada por:
Population Standard Deviation = √ (Σ (X i – X m ) 2 / n )
Caso você não receba toda a população e tenha apenas uma amostra (digamos que X seja o conjunto de dados de amostra da população), a fórmula para o desvio padrão da amostra será dada por:
Sample Standard Deviation = √ (Σ (X i – X m ) 2 / (n – 1))
Onde:
- X i - ésimo valor do conjunto de dados
- X m - valor médio do conjunto de dados
- n - número total de pontos de dados
A fórmula pode parecer confusa no começo, mas é realmente para trabalhar. A seguir estão as etapas que podem ser seguidas para calcular o desvio padrão da amostra:
- Encontre o número de pontos no conjunto de dados, ou seja, n
- O próximo passo é encontrar o valor médio da amostra. É basicamente a média de todos os valores.
- Depois disso, para cada ponto de dados, encontre a diferença disso em relação à média e depois faça o quadrado.
- Faça a soma de todos os valores na etapa acima e divida-os por n-1.
- O último passo é obter a raiz quadrada do número calculado acima.
Há outra maneira de calcular a população e o desvio padrão simplesmente usando a função DESVPAD.P () para desvio padrão da população e a função DESVPAD.S () para o desvio padrão da amostra no Excel.
Exemplos de fórmula de desvio padrão de amostra (com modelo do Excel)
Vamos dar um exemplo para entender melhor o cálculo do desvio padrão da amostra.
Você pode fazer o download deste modelo de amostra de fórmula de desvio padrão aqui - Modelo de amostra de fórmula de desvio padrãoExemplo de fórmula de desvio padrão - Exemplo # 1
Digamos que temos dois conjuntos de dados de amostra A e B e cada um contém 20 pontos de dados aleatórios e tem a mesma média. Calcular o desvio padrão da amostra para o conjunto de dados A e B.
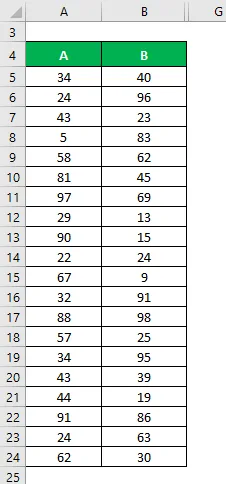
Solução:
A média é calculada como:
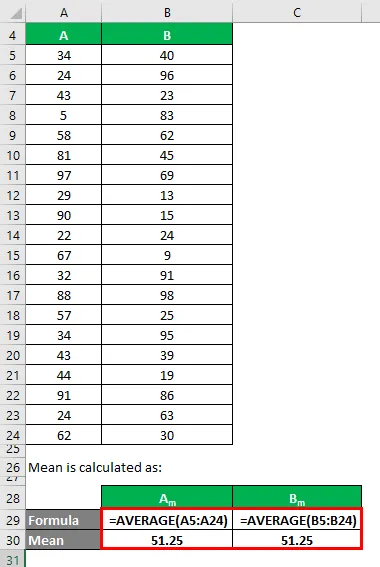
- Média do conjunto de dados A = 51, 25
- Média do conjunto de dados B = 51, 25
Agora, precisamos calcular a diferença entre os pontos de dados e o valor médio.
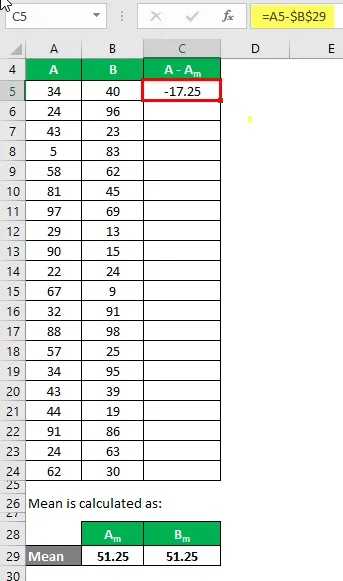
Da mesma forma, calcule para todo o conjunto de dados de A.
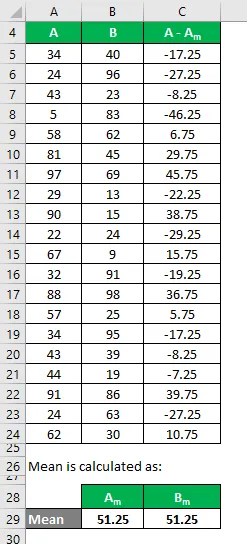
Da mesma forma, calcule-o para o conjunto de dados B também.
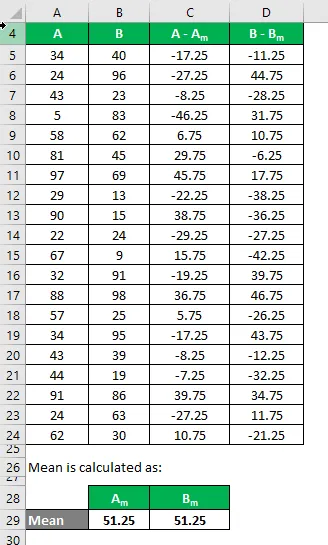
Calcule o quadrado da diferença para os conjuntos de dados A e B.
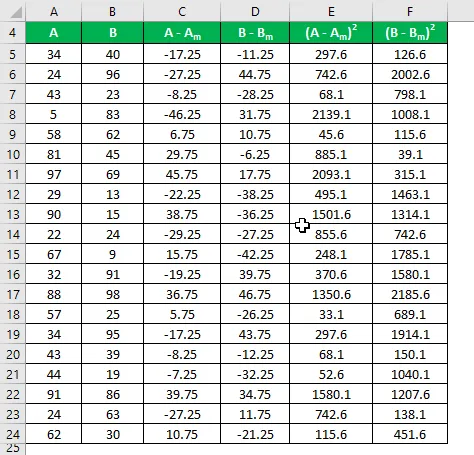
O desvio padrão da amostra é calculado usando a fórmula abaixo
Desvio padrão da amostra = √ (Σ (X i - X m ) 2 / (n - 1))
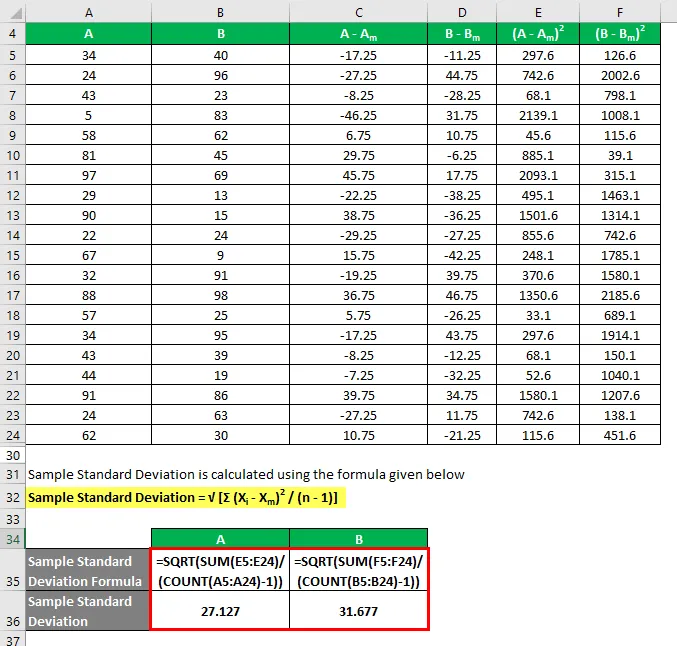
Portanto, se você vê aqui, embora ambos os conjuntos de dados tenham o mesmo valor médio, B tem um desvio mais padrão que A, o que significa que os pontos de dados de B são mais dispersos que A.
Fórmula de desvio padrão de amostra - Exemplo # 2
Digamos que você seja um investidor muito avesso ao risco e deseja investir dinheiro no mercado de ações. Como seu apetite por risco é baixo, você deseja investir em ações seguras com um desvio padrão mais baixo. Seu consultor financeiro sugeriu quatro ações para você escolher. Você deseja selecionar 2 ações entre as 4 e decidirá isso com base no menor desvio padrão.
Você tem informações sobre seus retornos históricos nos últimos 15 anos.
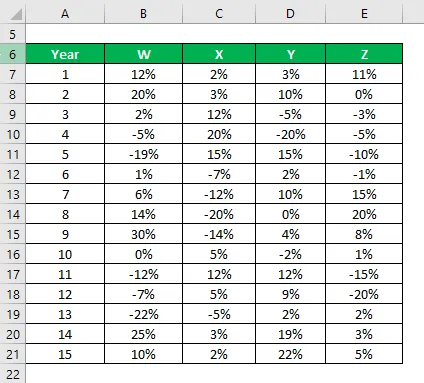
Solução:
O desvio padrão da amostra é calculado usando a fórmula do excel
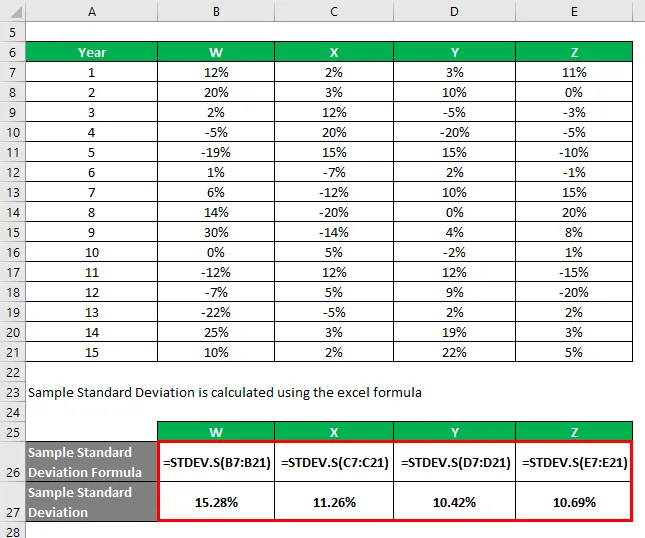
Com base nas informações e no desvio padrão da amostra, você escolherá o estoque Y e Z para investir, pois eles têm o menor desvio padrão.
Explicação
Discutimos o significado do desvio padrão do ponto de vista estatístico, mas também desempenha um papel vital se falarmos do ponto de vista financeiro. Em finanças, é basicamente a medida de risco que um investimento acarreta e quão arriscado é esse investimento. Com base no risco de um investimento, os investidores podem calcular o retorno mínimo necessário para compensar esse risco. Como no exemplo acima, como Y e Z têm um desvio padrão menor, isso significa que há menos variabilidade no retorno desses estoques, portanto eles são menos arriscados. Um ponto ao usar a ferramenta de desvio padrão, precisamos ter em mente que ela é altamente afetada pelos valores ou valores extremos. Esses valores extremos podem distorcer o valor do desvio padrão.
Relevância e usos da fórmula de desvio padrão da amostra
O desvio padrão ajuda os investidores e o analista a encontrar a relação de risco e recompensa ou a proporção de Sharpe para um investimento. Basicamente, qualquer pessoa pode obter uma taxa de retorno sem risco investindo em tesouraria e títulos sem risco. Mas o retorno acima e acima disso é o excesso de retorno e, para conseguir isso, qual é o nível de risco que se precisa correr é uma medida da razão Sharpe:
Razão Sharpe = (retorno do investimento - taxa livre de risco) / desvio padrão
Quanto maior a proporção de Sharpe, melhor é o investimento.
Como dissemos que o desvio padrão é uma medida de risco, mas o valor mais baixo do desvio padrão nem sempre é preferido. Se um investidor tem um apetite por risco mais alto e deseja investir de forma mais agressiva, ele estará disposto a correr mais riscos e preferir um desvio padrão relativamente mais alto do que um investidor avesso a riscos. Portanto, tudo depende do nível de risco que um investidor está disposto a assumir.
Artigos recomendados
Este foi um guia para a amostra da fórmula de desvio padrão. Aqui discutimos como calcular o desvio padrão da amostra, além de exemplos práticos e modelo de excel para download. Você também pode consultar os seguintes artigos para saber mais -
- Exemplos de fórmula de variação populacional
- Calculadora para desvio padrão relativo
- Como calcular a distribuição normal padrão?
- Cálculo da distribuição binomial