
Introdução à série Fibonacci em Python
Série Fibonacci em Python, isso é conhecido como uma série de números, onde o próximo número é a soma dos dois números atuais.
Por exemplo:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 .. so on
Então aqui 0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8+ 13 = 21 e assim por diante.
Olhando para o exposto, teríamos uma certa idéia sobre o que estamos falando.
No entanto, em termos de regra matemática, pode ser escrito como:

Onde enésimo número é a soma do número nos locais (n-1) e (n-2). Quando se trata de implementar a série Fibonacci, pode haver várias linguagens de codificação através das quais isso pode ser feito.
No entanto, o Python é uma linguagem amplamente usada atualmente. Vamos ver a implementação da série Fibonacci através do Python. Deve-se estar ciente de declarações de condicionamento básicas como loop, if-else, while loop, etc. em Python, antes de prosseguir aqui. Caso contrário, seria ótimo se alguém pudesse revisá-lo e depois pegar o conteúdo que viria. Aqui, para fins de demonstração, estou usando o spyder, que é IDE para a linguagem de programação python. Pode-se usar qualquer outro notebook IDE ou Ipython para a execução dos programas Python.
Série Fibonacci em Python
Vamos ver a implementação do número e da série de Fibonacci, considerando que os dois elementos de Fibonacci são 0 e 1:
No entanto, você pode ajustar a função de Fibonacci conforme sua exigência, mas consulte o básico primeiro e vá gradualmente para outros.
Código Python para encontrar o enésimo número de Fibonacci
Código 1:
def Fibonacci_num(m):
u = 0
v = 1
if m < 0:
print("Incorrect input entered")
elif m == 0:
return u
elif m == 1:
return v
else:
for i in range(2, m):
c = u + v
u = v
v = c
return v
Código 2:
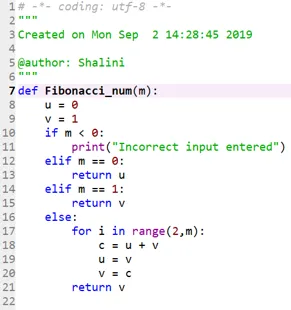
Resultado:
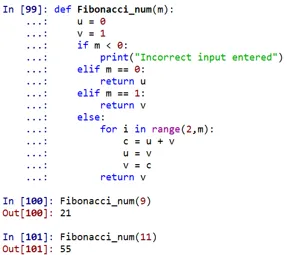
Como se pode ver, o número de Fibonacci no 9º lugar seria 21 e no 11º lugar seria 55.
- Aqui "fibonacci_num" é uma função definida, que cuida de encontrar o número de Fibonacci com a ajuda de determinadas condições. Esta função pode ser chamada especificando qualquer posição.
Agora vamos ver como se pode imprimir séries até a posição mencionada:
Código:
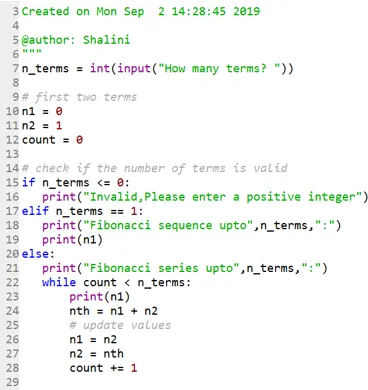
Resultado:
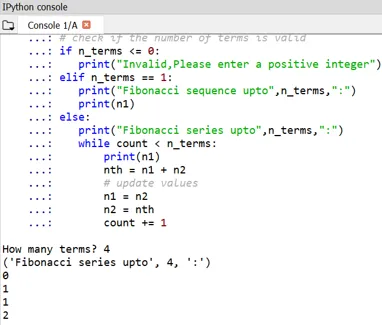
Pode-se notar que o início dos números de Fibonacci é definido como 0 e 1.
- Se alguém quiser definir seus próprios termos iniciais, isso também pode ser feito da mesma maneira, ajustando n1 e n2. Aqui está o exemplo disso:
Digamos que agora queremos que nossos termos iniciais sejam: n1 = 3, n2 = 5
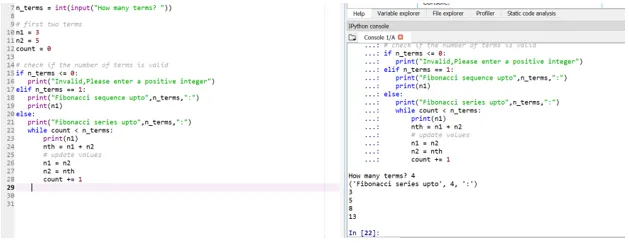
Portanto, aqui a sua posição do 4º termo (a entrada do usuário é tomada) será decidida com base nos seus termos iniciais.
Métodos através dos quais a série Fibonacci pode ser gerada
Abaixo estão os três métodos pelos quais as séries de Fibonacci podem ser geradas:
1. Através de geradores
Código:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
Resultado:
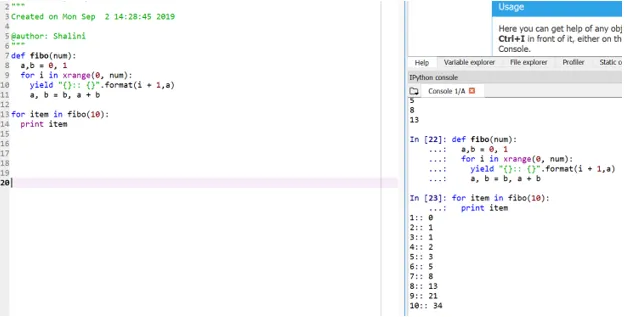
Este método é chamado de "gerador" porque a função xrange é um gerador de números entre 0 e num e yield é o gerador de saída formatada.
Aqui está o que o xrange faz por você:

Aqui, a série Fibonacci foi definida na forma de função, dentro da qual as funções loop, xrange e yield cuidam da saída.
2. Através de loop
Código:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
Resultado:

Como se pode ver, o loop for simples foi usado, para imprimir a série Fibonacci entre 0 e 10. No loop for interno, novos valores foram atribuídos às variáveis. U e v são os valores iniciais padrão de Fibonacci que foram configurados para 0 e 1, respectivamente.
Quanto ao loop progredir para execução, o novo valor u é o antigo valor v, enquanto o novo valor v é a soma dos valores antigos de u e v. Isso continua até o final dos valores do intervalo.
3. Através da recursão
Código:
#Through recursion
def fibonacci_ser(m):
if(m <= 1):
return m
else:
return(fibonacci_ser(m-1) + fibonacci_ser(m-2))
m = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(m):
print fibonacci_ser(i),
Resultado:
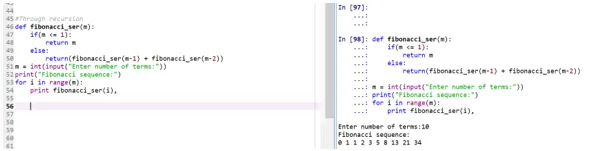
- A função "fibonacci_ser" está fazendo a chamada para imprimir a série Fibonacci.
- E, portanto, o método recebeu o nome de "recursão".
Passos seguidos aqui:
- Aqui, o usuário foi solicitado a inserir o local até o qual a série Fibonacci precisa ser impressa.
- O número passa pela função "fibonacci_ser".
- A condição é verificada, se o comprimento fornecido for menor que 1 ou não. Se sim, o resultado é dado imediatamente.
- No entanto, se o comprimento for maior que 1, chamadas recursivas serão feitas para "fibonacci_ser" com argumentos com comprimento menor que 1 e 2, ou seja, fibonacci_ser (m-1) e fibonacci_ser (m-2).
- Portanto, a recursão fornece a saída desejada e a imprime.
- Então, em resumo, discutimos três maneiras de exibir a série Fibonacci.
- Através de loop for, geradores e recursão.
Todos os três códigos Python resumidos
Abaixo estão os três códigos python:
1. Através de geradores
Código:
def fibo(num):
a, b = 0, 1
for i in xrange(0, num):
yield "():: ()".format(i + 1, a)
a, b = b, a + b
for item in fibo(10):
print item
2. Através de loop
Código:
u, v = 0, 1
for i in xrange(0, 10):
print u
u, v = v, u + v
3. Através da recursão
Código:
def fibonacci_ser(n):
if(n <= 1):
return n
else:
return(fibonacci_ser(n-1) + fibonacci_ser(n-2))
n = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(n):
print fibonacci_ser(i),
Resumidos acima, estão todos os procedimentos, é preciso praticar para obter uma boa compreensão de todos.
Resultado:
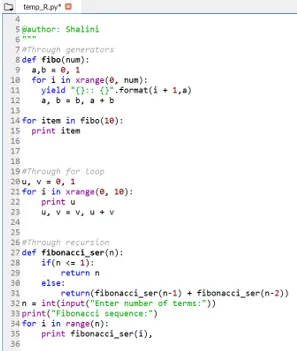
Conclusão
Passando pelo conteúdo acima de Fibonacci, teríamos uma compreensão clara dos números e séries de Fibonacci, especializados em python. Uma vez, a pessoa se sente à vontade com a lógica da série Fibonacci, gerando outro conjunto de séries, trabalhando com outros números e com vários métodos, agora será uma tarefa fácil para você. Uma abordagem lógica é a única maneira de se destacar nisso.
Artigos recomendados
Este é um guia para a série Fibonacci em Python. Aqui discutimos números e séries de Fibonacci, especializados em python, gerando outro conjunto de séries, trabalhando com outros números e com vários métodos. Você também pode consultar nossos outros artigos relacionados para saber mais -
- Gerador de número aleatório em Python
- Funções matemáticas em Python
- Fatorial em Python
- Encapsulamento em Python
- Série Fibonacci em Java
- Recursos do Python
- Programa fatorial em JavaScript
- Gerador de número aleatório no Matlab
- Gerador de número aleatório em c #
- Encapsulamento em JavaScript