
Introdução aos exemplos de desvio padrão
Existem amplos exemplos de desvios padrão. O desvio padrão é a medida da dispersão do conjunto de dados, ou seja, a distribuição dos números. É útil para comparar os diferentes conjuntos de dados que podem ter a mesma média, mas o intervalo diferente. O seguinte exemplo de desvio padrão diferente fornece um entendimento sobre o tipo mais comum de situações em que o desvio padrão é calculado e como se pode calcular o mesmo
Exemplos de desvio padrão
Abaixo estão os exemplos do desvio padrão
Desvio Padrão - Exemplo # 1
O estoque da empresa Z é vendido por US $ 50 por ação e as mesmas ofertas após os pagamentos do próximo ano:
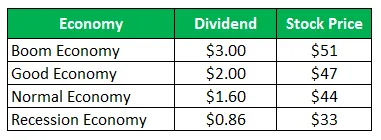
Calcule o desvio padrão quando todos os quatro cenários forem igualmente prováveis.
Solução:
Os cálculos do retorno do período de retenção (HPR) são os seguintes:
Fórmula de HPR
HPR = ((Valor no final do período - Valor original) + Renda) / Valor original) * 100
Para economia da lança
- HPR (Lança) = ((51-50) + 3) / 50 = 8, 00%
- HPR (Bom) = ((47-50) + 2) / 50 = -2, 00%
- HPR (Normal) = ((44-50) + 1, 60) / 50 = -8, 80%
- HPR (recessão) = ((33-50) + 0, 86) / 50 = -32, 28%
Cálculo do retorno esperado
Como todos os cenários são igualmente prováveis, a probabilidade de todos será ¼
Fórmula de Retorno Esperado
Retorno esperado = (probabilidade de crescimento * retorno do crescimento) + (probabilidade de bom * retorno do bem) + (probabilidade de normal * retorno do normal) + (probabilidade de recessão * retorno da recessão)
- Retorno esperado = (1/4 x 8%) + (1/4 x -2%) + (1/4 x -8, 80%) + (1/4 x -32, 28%)
- Retorno Esperado = -8, 77%
Cálculo do desvio padrão
Fórmula de variância
Variação = (probabilidade de crescimento * (retorno do crescimento - retorno total esperado) 2) + (probabilidade de bem * (retorno do bem - retorno total esperado) 2) + (probabilidade de normal * (retorno do normal - retorno total esperado)) 2 ) + (Probabilidade de recessão * (retorno da recessão - retorno total esperado) 2)
- Variação = 1/4 (8 - (-8, 77)) 2 + 1/4 (-2 - (-8, 77)) 2 + 1/4 (-8, 80 - (-8, 77)) 2 + 1/4 (-32, 28 - (-8, 77)) 2
- Variação = 219, 95
Fórmula do desvio padrão
O desvio padrão será a raiz quadrada da variação
Desvio padrão = √Variância
- Desvio padrão = √ 219, 95
- Desvio Padrão = 14, 83%
Exemplo de desvio padrão - 2
Desvio padrão no caso de duas empresas do portfólio
As ações ordinárias da empresa A são vendidas por US $ 28 por ação e as mesmas ofertas após os pagamentos do próximo ano

As ações ordinárias da Empresa B são vendidas por US $ 93 por ação e as mesmas ofertas após os pagamentos do próximo ano:

(a) Calcule o desvio padrão da empresa A
(b) Calcule o desvio padrão da empresa B
(c) Calcule o desvio padrão da carteira se metade do investimento for realizado na Empresa A e restante na Empresa B
Solução:
Para a empresa A
Cálculos do retorno do período de espera (HPR)
Fórmula de HPR
HPR = ((Valor no final do período - Valor original) + Renda) / Valor original) * 100
- HPR (boom) = ((20-28) + 1) / 28 = -25, 00%
- HPR (Normal) = ((30-28) + 1, 50 / 28 = 12, 50%
- HPR (recessão) = ((38-28) + 5) / 28 = 53, 57%
Cálculo do retorno esperado da empresa A
Fórmula de Retorno Esperado
Retorno esperado = (probabilidade de crescimento * retorno do crescimento) + (probabilidade de normal * retorno do normal) + (probabilidade de recessão * retorno da recessão)
- Retorno esperado = (0, 45 x -25, 00%) + (0, 35 x 12, 50%) + (0, 20 x 53, 57%)
- Retorno esperado = 3, 84%
Cálculo da empresa de desvio padrão A
Fórmula de variância
Variação = (Probabilidade de crescimento * (retorno da lança - retorno total esperado) 2) + (Probabilidade de normal * (retorno do normal - retorno total esperado) 2 ) + (Probabilidade de recessão * (retorno da recessão - retorno total esperado)) 2)
- Variação = 0, 45 (-25, 00 - (3, 84)) 2 + 0, 35 (12, 50 - (3, 84)) 2 + 0, 20 (53, 57 - (3, 84)) 2
- Variação = 895, 15
Fórmula do desvio padrão
O desvio padrão será a raiz quadrada da variação
Desvio padrão = √Variância
- Desvio padrão = √ 895, 15
- Desvio Padrão = 29, 92%
Para a empresa B
Cálculos do retorno do período de espera (HPR)
Fórmula de HPR
HPR = ((Valor no final do período - Valor original) + Renda) / Valor original) * 100
HPR (Lança) = ((200-93) +7) / 93 = 122, 58%
HPR (Normal) = ((105-93) + 5, 50 / 93 = 18, 82%
HPR (recessão) = ((4-93) +2) / 93 = -93, 55%
Cálculo do retorno esperado
Fórmula de Retorno Esperado
Retorno esperado = (probabilidade de crescimento * retorno do crescimento) + (probabilidade de normal * retorno do normal) + (probabilidade de recessão * retorno da recessão)
- Retorno esperado = (0, 45x 122, 58%) + (0, 35 x 18, 82%) + (0, 20 x -93, 55%)
- Retorno Esperado = 43, 04%
Cálculo do desvio padrão
Fórmula de variância
Variação = (Probabilidade de crescimento * (retorno da lança - retorno total esperado) 2) + (Probabilidade de normal * (retorno do normal - retorno total esperado) 2 ) + (Probabilidade de recessão * (retorno da recessão - retorno total esperado)) 2)
- Variação = 0, 45 (122, 58– (43, 04)) 2 + 0, 35 (18, 82– (43, 04)) 2 + 0, 20 (-93, 55– (43, 04)) 2
- Variação = 6783, 65
Fórmula do desvio padrão
O desvio padrão será a raiz quadrada da variação
Desvio padrão = √Variância
- Desvio padrão = √6783, 65
- Desvio Padrão = 82, 36%
Cálculo do retorno esperado e do desvio padrão de uma carteira metade investida na empresa A e metade na empresa B.
Desvio Padrão da Empresa A = 29, 92%
Desvio Padrão da Empresa B = 82, 36%
Peso da empresa A = 0, 50
Peso da empresa B = 0, 50
A fórmula do desvio padrão do portfólio
Desvio padrão do portfólio = (Peso da empresa A * retorno esperado da empresa A) + ((Peso da empresa B * retorno esperado da empresa B))
- Desvio padrão do portfólio = (0, 50 * 29, 92) + (0, 50 * 82, 36)
- Desvio Padrão do Portfólio = 56, 14%
Análise
O desvio padrão do portfólio é menor do que para o indivíduo de uma ação, porque as ações são diversificadas em ações diferentes. A diversificação leva a uma redução no risco, a menos que exista uma correlação perfeita entre os retornos dos investimentos do portfólio.
Conclusão - Exemplos de desvio padrão
O desvio padrão mede a dispersão do conjunto de dados que é relativa à sua média. É calculado como a raiz quadrada da variação. Quanto maior o desvio padrão do título, maior será a variação entre cada preço e a média, o que mostra que a faixa de preço é grande. Os exemplos acima mencionados são alguns dos exemplos de desvio padrão de diferentes maneiras. Existem vários outros exemplos que mostram que o desvio padrão pode ser calculado usando outros dados.
Artigos recomendados
Este foi um guia para os exemplos de desvio padrão. Aqui discutimos os vários exemplos de desvio padrão, juntamente com uma explicação detalhada . Você também pode consultar os seguintes artigos para saber mais -
- Exemplo de custos fixos
- Exemplo de custo variável
- Exemplo de Pesquisa Quantitativa
- Exemplos de concorrência monopolística