
Introdução à função recursiva em Java
Uma função recursiva é aquela que se chama uma ou várias vezes. Uma função recursiva é usada em situações em que o mesmo conjunto de operações precisa ser executado repetidamente até o resultado ser alcançado. Ele realiza várias iterações e a declaração do problema continua se tornando mais simples a cada iteração.
Sempre um limite base deve ser especificado ao escrever uma função recursiva, caso contrário, isso resulta em erro de estouro de pilha. Uma pilha é uma área de memória reservada para manter invocações de métodos. O erro ocorre porque a função começa a executar continuamente, pois não conseguirá encontrar a condição limitadora e, portanto, esgotará a memória alocada. Portanto, para evitar o estouro de pilha, definimos certas condições básicas com a ajuda de instruções "if … else" (ou quaisquer outras instruções condicionais) que fazem com que a função de recursão pare assim que a computação necessária for concluída.
Tipos de recursão em Java
Existem 2 tipos de recursão em Java. Eles são:
1. Recursão Direta
Sintaxe:
Aqui a função1 se chama continuamente, portanto, é uma função recursiva.
public static void main(String() args)(
//few lines of code
function();
//few lines of code
)
function() (
//few lines of code
function();
//few lines of code
)
Exemplo
O fatorial de um número é um exemplo de recursão direta. O princípio básico da recursão é resolver um problema complexo, dividindo-o em problemas menores. Por exemplo, no caso de fatorial de um número, calculamos o fatorial de "i" se conhecermos o fatorial de "i-1".
Código:
public class Factorial (
static int fact(int i)(
if (i == 1)
return 1;
else
return(i * fact(i-1));
)
public static void main(String() args) (
System.out.println("The factorial of given number 6 is: "+fact(6));
)
)
Resultado:

2. Recursão Indireta / Mútua
Uma função1 que chama outra função2, que por sua vez chama função1, direta ou indiretamente, é chamada função recursiva indireta.
Sintaxe:
Considere 2 funções chamadas function1 () e function2 (). Aqui, a função1 chama função2 e a função2 chama função1.
function1()(
//few lines of code
function2();
//few lines of code
)
function2()(
//few lines of code
function1();
//few lines of code
)
Exemplo
Para mostrar recursão indireta, tomamos o programa a seguir usado para descobrir se um determinado número é par ou ímpar da entrada fornecida.
Código:
import java.util.Scanner;
public class IndirectRecursion (
public static boolean oddNum(int i) (
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0)(
return false;
) else (
return evenNum(i-1);
)
)
public static boolean evenNum(int i) (
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0)(
return true;
) else (
return oddNum(i-1);
)
)
public static void main(String() args) (
Scanner inputNum = new Scanner(System.in);
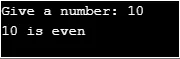
System.out.print("Give a number: ");
int n = inputNum.nextInt();
if (evenNum(n)) System.out.println(n + " is even");
else System.out.println(n + " is odd");
inputNum.close();
)
)
Resultado:
Exemplos de recursão em Java
Aqui estão mais alguns exemplos para resolver os problemas usando o método de recursão.
Exemplo # 1 - Sequência de Fibonacci
Diz-se que um conjunto de números "n" está em uma sequência de Fibonacci se número3 = número1 + número2, isto é, cada número é uma soma dos dois números anteriores. Portanto, a sequência sempre começa com os dois primeiros dígitos, como 0 e 1. O terceiro dígito é uma soma de 0 e 1, resultando em 1, o quarto número é a adição de 1 e 1, resultando em 2, e a sequência continua.
Confira o seguinte código em Java para gerar uma sequência de Fibonacci:
public class FibonacciSeries(
static int num1=0, num2=1, num3=0;
static void fibonacci(int n)(
if(n>0)(
num3 = num1 + num2;
num1 = num2;
num2 = num3;
System.out.print(" "+num3);
fibonacci(n-1);
)
)
public static void main(String args())(
int n=10;
System.out.print(num1+" "+num2);//printing constant first two digits 0 and 1
fibonacci(n-2);//Since first two numbers are already done
)
)
Resultado:

Aqui os dois primeiros números são inicializados em 0 e 1 e impressos. As variáveis "num1", "num2" e "num3" são usadas para gerar a sequência necessária. A variável "num3" é obtida adicionando "num1" e "num2" e os números são deslocados uma posição para a esquerda, baralhando conforme mostrado no código. A função "Fibonacci" é chamada recursivamente aqui e a cada iteração, o valor de "n" é diminuído em 1. Portanto, a recursão sai assim que "n" atinge o valor 0.
Exemplo # 2 - Torre de Hanói
Esse é um problema matemático clássico que possui 3 pólos e o número "n" de discos com tamanhos diferentes. O quebra-cabeça é o seguinte:
No início, o primeiro pólo terá os discos dispostos de forma que o maior disco de todos esteja na parte inferior e o menor no topo do pólo. O objetivo é mover esses discos do primeiro para o terceiro, mantendo os discos na mesma posição do primeiro. A seguir, algumas condições a serem lembradas ao trocar esses discos:
1. Por vez, apenas um disco deve ser movido.
2. No processo, não é permitido colocar um disco maior sobre um menor.
3. O segundo pólo (do meio) pode ser usado para mediar enquanto transfere os discos do primeiro para o segundo pólo.
A seguir está o código Java que pode ser usado para resolver o quebra-cabeça:
Código:
public class TowerOfHanoi (
public static void main(String() args) (
int count = 3;
tower(count, 'A', 'B', 'C');
)
public static void tower(int first, char disk1, char temp, char disk2) (
if (first == 1) (
System.out.println("Disk 1 from " + disk1 + " to " + disk2);
) else (
tower(first - 1, disk1, disk2, temp);
System.out.println("Disk " + first + " from " + disk1 + " to " + disk2);
tower(first - 1, temp, disk1, disk2);
)
)
)
Resultado:
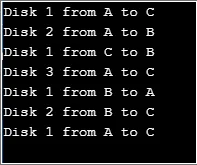
Aqui a variável "count" representa o número de discos a serem utilizados. A função “torre” é a função recursiva usada para mover os discos da haste 1 para a haste 3. Uma solução simples para esse problema pode ser fornecida considerando dois discos no início.
- Primeiro, começamos movendo o disco1 da haste 1 para a haste 2.
- Em seguida, movemos o disco2 para a haste 3.
- Finalmente, terminamos movendo o disco1 para a haste 3, completando a solução necessária.
Esse mesmo princípio é aplicado ao número “n” de discos movendo (n-1) o disco da haste 1 para 2 e seguindo etapas semelhantes às acima.
Vantagens da recursão em Java
- O código é fácil de escrever e manter.
- O melhor método para encontrar os resultados em que é necessário um grande número de iterações.
Desvantagens da recursão em Java
- Funções recursivas usam mais memória. Isso ocorre sempre que uma função recursiva é chamada; a alocação de memória é feita recentemente para as variáveis na pilha. E a respectiva alocação de memória é liberada assim que os valores das variáveis são retornados.
- Esse processo de alocação de memória leva mais tempo, portanto, a execução geralmente é lenta.
Conclusão
Funções recursivas são relativamente mais simples de codificar, mas também não são tão eficientes em comparação com os outros métodos existentes. Portanto, eles são usados principalmente nos casos em que o tempo concedido para o desenvolvimento é menor e também onde um padrão significativo pode ser observado no problema.
Artigos recomendados
Este é um guia para recursão em Java. Aqui discutimos os tipos de recursão em Java, juntamente com seus diferentes exemplos, com as vantagens e desvantagens. Você também pode consultar os seguintes artigos para saber mais:
- JScrollPane em Java
- Funções matemáticas em Java
- Funções matemáticas em Java
- Construtor em Java
- Função Recursiva em Python
- Programa fatorial em JavaScript