Fórmula de Taxa Anual Efetiva (Sumário)
- Fórmula
- Exemplos
- Calculadora
Qual é a fórmula da taxa anual efetiva?
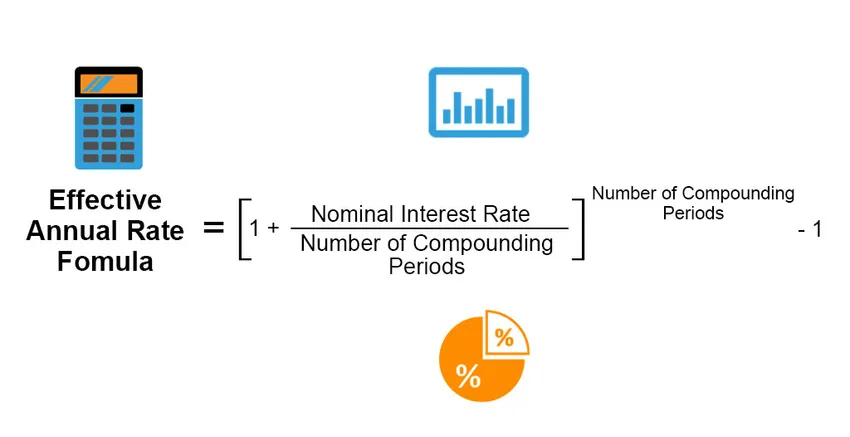
Taxa Anual Efetiva é a taxa de juros real auferida ou paga em um investimento, empréstimo ou qualquer outro produto financeiro semelhante e, caso contrário, é diferente da "Taxa de juros nominal" devido ao período de pagamento dos juros, composto pela taxa de juros, total período de tempo do empréstimo ou investimento, etc. A taxa anual efetiva é calculada pela seguinte fórmula;
Effective Annual Rate = ((1 + (Nominal Interest Rate / Number of Compounding Periods)) Number of Compounding Periods) – 1
Exemplos de fórmula de taxa anual efetiva (com modelo do Excel)
Vamos dar um exemplo para entender melhor o cálculo da Taxa Anual Efetiva.
Você pode baixar este modelo de fórmula de taxa anual efetiva do Excel aqui - modelo de fórmula de taxa anual efetivaFórmula de taxa anual efetiva - Exemplo # 1
Suponha que o Sr. X contrate um empréstimo pessoal de um banco com uma taxa de juros de 20%, composta semestralmente. Calcule a taxa anual efetiva usando as informações.

Solução:
A taxa anual efetiva é calculada usando a fórmula abaixo
Taxa anual efetiva = ((1 + (Taxa de juros nominal / número de períodos compostos)) Número de períodos compostos) - 1

- Taxa anual efetiva = ((1 + (20% / 2)) 2) - 1
- Taxa anual efetiva = 21%
Fórmula de taxa anual efetiva - exemplo nº 2
Suponha que o Sr. A investiu US $ 100 em um certificado de depósito que pague uma taxa de juros nominal anual de 10%, composta trimestralmente. Calcular a taxa anual efetiva.

Solução:
A taxa anual efetiva é calculada usando a fórmula abaixo
Taxa anual efetiva = ((1 + (Taxa de juros nominal / número de períodos compostos)) Número de períodos compostos) - 1
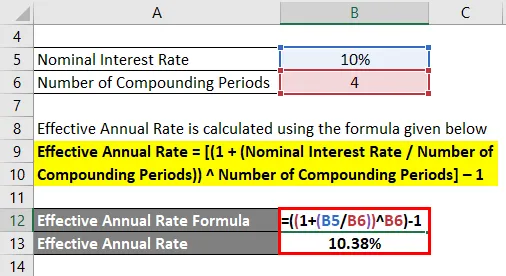
- Taxa anual efetiva = ((1 + (10% / 4)) 4) - 1
- Taxa anual efetiva = 10, 38%
Fórmula de taxa anual efetiva - exemplo nº 3
Vamos supor que o investimento em fundos mútuos busque uma taxa de juros anual de 15, 50% como lucro, enquanto o P2P Lending ganha uma taxa de juros nominal anual de 15%, composta mensalmente. Portanto, calcule a taxa anual efetiva para ambos os casos.

Solução:
A taxa anual efetiva é calculada usando a fórmula abaixo
Taxa anual efetiva = ((1 + (Taxa de juros nominal / número de períodos compostos)) Número de períodos compostos) - 1
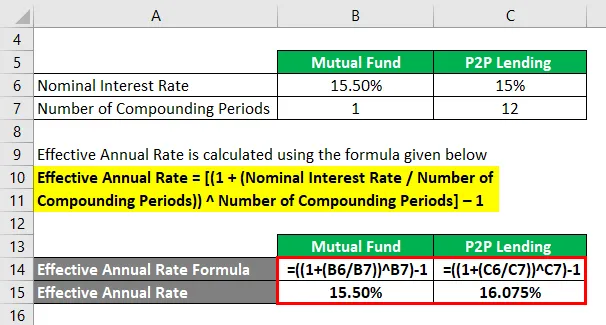
Para Fundo Mútuo
- Taxa anual efetiva = ((1 + (15, 50% / 1)) 1) - 1
- Taxa anual efetiva = 15, 50%
Para empréstimos P2P
- Taxa anual efetiva = ((1 + (15% / 12)) 12) - 1
- Taxa anual efetiva = 16, 075%
Explicação
A taxa de juros nominal é a taxa declarada no produto financeiro. No Exemplo 3, a taxa nominal exibida nos produtos faz com que o Fundo Mútuo pareça a escolha preferida de investimento para os investidores, devido à taxa nominal anual de juros 0, 50% maior.
No entanto, a taxa anual efetiva é calculada tomando a taxa de juros anual nominal e compondo-a pelo número de períodos especificados (12 se a composição for mensal; 6 se a composição for bimensal; 4 se for trimestral; e 2 se for é semestral) aplicável no período de um ano. No caso do fundo mútuo, o número de períodos compostos por ano é 1, enquanto no caso de empréstimos P2P, é composto mensalmente, portanto, existem 12 períodos compostos.
Com base na fórmula,
Retornos anuais efetivos = ((1 + (taxa de juros nominal / número de períodos compostos)) (número de períodos compostos)) - 1
Retorno anual efetivo do fundo de investimento = ((1 + (15, 50% / 1)) 1) - 1 = 15, 50%
Retorno anual efetivo do empréstimo de P2P = ((1 + (15, 00% / 12)) 12) - 1 = 16, 075%
Relevância e usos da fórmula efetiva da taxa anual
A fórmula da taxa anual efetiva é usada para distinguir a TIR real (Taxa Interna de Retorno) ou o rendimento anualizado de uma taxa de juros que pode ou não ser composta várias vezes durante um determinado período. Isso poderia ser muito bem utilizado na comparação de diferentes tipos de oportunidades de investimento ou de empréstimos concedidos sob diferentes estruturas.
Vamos supor que existem 2 oportunidades de investimento, Depósitos a Prazo dos Correios e Depósitos Fixos Bancários nos quais um investidor reduziu, considerando seu apetite e adequação ao risco. O objetivo final do investidor é tirar o máximo proveito desses depósitos e obter um retorno maior. No entanto, ambos os instrumentos oferecem taxas de juros ligeiramente diferentes, enquanto o Depósito a Prazo dos Correios oferece composição trimestral para o prazo considerado.
- Valor do investimento: Rs. 10 lakhs
- Período de investimento: 5 anos
- Depósito Fixo Bancário: Juros Anuais a 7, 5%
- Depósito a Prazo dos Correios: Juros Anuais de 7, 4%, compostos trimestralmente
Pela aparência das taxas de juros anuais oferecidas, o Depósito Fixo Bancário parece ser a melhor opção. No entanto, se o investidor realmente calcular o fator de composição trimestral do Depósito a Prazo dos Correios, isso resultará em uma taxa / retorno anual efetivo de 7, 61%.
Devido a essa pequena mudança de 7, 4% para 7, 61% na taxa efetiva, o investidor ganharia um total de Rs. 4, 42, 848.28 deste instrumento em particular, enquanto ele / ela teria ganho Rs. 3, 35, 469.14 do instrumento Depósito Fixo Bancário.
Se o investidor deixar de calcular essa taxa anual efetiva, ele / ela teria perdido a oportunidade de ganhar aproximadamente mais de Rs. 1 lakh de seu investimento.
Calculadora de fórmula de taxa anual efetiva
Você pode usar a seguinte calculadora de taxa anual efetiva
| Taxa de interesse nominal | |
| Número de períodos compostos | |
| Taxa anual efetiva | |
| Taxa anual efetiva = | ((1 + (Taxa de juros nominal / número de períodos compostos)) Número de períodos compostos ) - 1 | |
| ((1 + (0/0)) 0 ) - 1 = | 0 0 |
Artigos recomendados
Este é um guia para a fórmula de taxa anual efetiva. Aqui discutimos como calcular a taxa anual efetiva, juntamente com exemplos práticos. Também fornecemos uma Calculadora de Taxa Anual Efetiva com modelo excel para download. Você também pode consultar os seguintes artigos para saber mais -
- Calculadora para fórmula de taxa de juros real
- Fórmula de retorno do capital empregado | Definição
- Como calcular a taxa de juros efetiva?
- Qual é o valor presente da fórmula da anuidade?