
Fórmula de distribuição de Poisson (Sumário)
- Fórmula
- Exemplos
- Calculadora
O que é a fórmula de distribuição de Poisson?
Em Probabilidade e Estatística, existem três tipos de distribuições baseadas em dados contínuos e discretos - Normal, Binomial e Poisson. A distribuição normal é frequentemente como uma curva de sino. Distribuição de Poisson, freqüentemente chamada de Distribuição de eventos raros. Isso é usado predominantemente para prever a probabilidade de eventos que ocorrerão com base na frequência com que o evento aconteceu no passado. Permite a ocorrência de um determinado número de eventos em um conjunto de períodos. É usado em muitas situações da vida real.
A fórmula para encontrar a distribuição de Poisson é dada abaixo:
P(x) = (e -λ * λ x) / x!
Para x = 0, 1, 2, 3…
Esse experimento geralmente conta o número de eventos ocorridos na área, distância ou volume. Junto com isso, pode-se encontrar a Cadeia de eventos que nada mais é que a cadeia de ocorrências do mesmo evento durante o período de tempo específico. A distribuição de Poisson possui as seguintes características comuns.
- Um evento pode acontecer a qualquer momento e a qualquer momento.
- O evento pode considerar medidas como volume, área, distância e tempo.
- No entanto, a probabilidade de um evento ocorrer em qualquer medida especificada acima é a mesma.
- Cada evento não depende de todos os outros eventos, o que significa que a probabilidade de um evento acontecer não afeta outro evento ao mesmo tempo.
Exemplos de fórmula de distribuição de Poisson
Vamos dar um exemplo para entender melhor o cálculo da distribuição de Poisson.
Você pode fazer o download deste modelo de Excel de fórmula de distribuição de Poisson aqui - Modelo de Excel de fórmula de distribuição de PoissonFórmula de distribuição de Poisson - Exemplo # 1
O número médio de acidentes anuais ocorridos na plataforma da estação ferroviária durante o movimento do trem é 7. Para identificar a probabilidade de que haja exatamente 4 incidentes na mesma plataforma este ano, a fórmula de distribuição de Poisson pode ser usada.
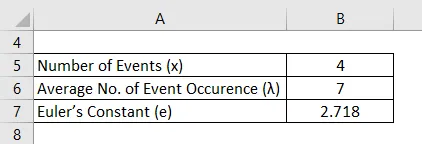
Solução:
A distribuição de Poisson é calculada usando a fórmula abaixo
P (x) = (e -λ * λ x) / x!
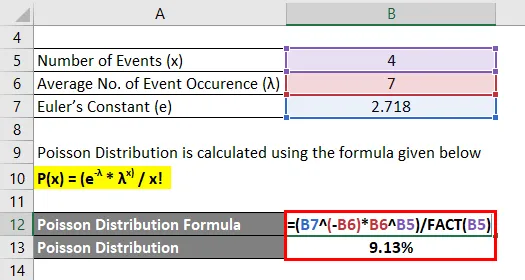
- P (4) = (2, 718 -7 * 7 4) / 4!
- P (4) = 9, 13%
Para o exemplo dado, há 9, 13% de chances de que ocorra exatamente o mesmo número de acidentes que pode ocorrer este ano.
Fórmula de distribuição de Poisson - Exemplo # 2
O número de erros de digitação cometidos por um datilógrafo possui uma distribuição de Poisson. Os erros são cometidos de forma independente a uma taxa média de 2 por página. Encontre a probabilidade de uma carta de três páginas não conter erros.
Aqui taxa média por página = 2 e taxa média de 3 páginas (λ) = 6
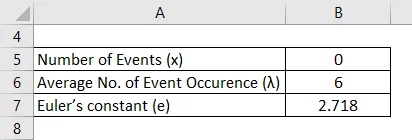
Solução:
A distribuição de Poisson é calculada usando a fórmula abaixo
P (x) = (e -λ * λ x) / x!
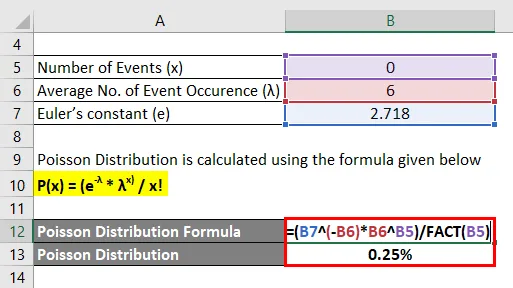
- P (0) = (2, 718 -6 * 6 0 ) / 0!
- P (0) = 0, 25%
Portanto, há 0, 25% de chances de que não haja erros em 3 páginas.
Nota : x 0 = 1 (qualquer valor de potência 0 será sempre 1) ; 0! = 1 (fatorial zero será sempre 1)Explicação
Abaixo está a abordagem passo a passo para calcular a fórmula de distribuição de Poisson.
Etapa 1: e é a constante de Euler, que é uma constante matemática. Geralmente, o valor de e é 2, 718 .
Etapa 2: X é o número de eventos reais ocorridos. Pode ter valores como os seguintes. x = 0, 1, 2, 3…
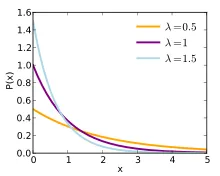
Etapa 3: λ é o número médio (médio) de eventos (também conhecido como “Parâmetro da distribuição de Poisson). Se você usar o exemplo simples para calcular λ => 1, 2, 3, 4, 5. Se você aplicar o mesmo conjunto de dados na fórmula acima, n = 5, portanto, média = (1 + 2 + 3 + 4 + 5) / 5 = 3. Para um grande número de dados, não é possível encontrar a mediana manualmente. Portanto, é essencial usar a fórmula para um grande número de conjuntos de dados. Aqui no cálculo da distribuição de Poisson, normalmente obteremos o número médio diretamente. Com base no valor de λ, o gráfico de Poisson pode ser unimodal ou bimodal como abaixo.
Etapa 4: x! é o fatorial dos eventos reais ocorridos x. Abaixo está um exemplo de como calcular fatorial para o número fornecido.
Se você usar o exemplo simples para calcular o fatorial do conjunto de dados reais => 1, 2, 3, 4, 5.
- x! = x * (x-1) * (x-2) * (x-3) * …… 3 * 2 * 1
- 5! = 5 * (5-1) * (5-2) * (5-3) * (5-4)
- 5! = 5 * 4 * 3 * 2 * 1
- 5! = 120
Relevância e usos da fórmula de distribuição de Poisson
A distribuição de Poisson pode funcionar se o conjunto de dados for uma distribuição discreta, cada ocorrência for independente das outras ocorrências ocorridas, descrever eventos discretos ao longo de um intervalo, eventos em cada intervalo podem variar de zero a infinito e significar que várias ocorrências devem ser constante ao longo do processo. Dependendo do valor do Parâmetro (λ), a distribuição pode ser unimodal ou bimodal. A distribuição de Poisson é uma distribuição discreta, significa que o evento só pode ser declarado como acontecendo ou não, o que significa que o número só pode ser indicado em números inteiros. As ocorrências fracionárias do evento não fazem parte deste modelo. Os resultados do resultado podem ser classificados como sucesso ou fracasso. Isso é amplamente usado no mundo de:
- Análise de dados para análise preditiva de dados
- Previsões do mercado de ações
- Previsões do mercado de vendas
- Previsões da cadeia de suprimentos e demanda
- Prontamente disponível nas plataformas Amazon Web Services (AWS)
- Revisar e avaliar a cobertura de seguro comercial
Outras aplicações da distribuição Poisson são de problemas mais abertos. Por exemplo, ele pode ser usado para ajudar a determinar a quantidade mínima de recursos necessários em um call center com base na média de chamadas recebidas e em espera. Em resumo, a lista de aplicativos pode ser adicionada cada vez mais, pois é usada para fins estatísticos práticos em todo o mundo.
Calculadora de fórmula de distribuição de Poisson
Você pode usar a seguinte calculadora de distribuição de Poisson
| λ | |
| x | |
| P (x) | |
| P (x) = | (e- λ * λ x ) / x! | |
| (0 -0 * 0 0 ) / 0! = | 0 0 |
Fórmula de distribuição de Poisson no Excel (com modelo do Excel)
Aqui faremos outro exemplo da distribuição de Poisson no Excel. É muito fácil e simples.
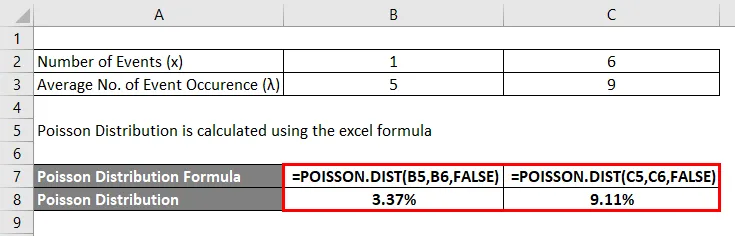
Calcule a distribuição de Poisson no Excel usando a função POISSON.DIST.
Abaixo está a fórmula Sintaxe da distribuição de Poisson no Excel.

A distribuição de Poisson tem o seguinte argumento:
Onde,
- x = Número de ocorrências cuja probabilidade precisa ser conhecida.
- Média = número médio de ocorrências durante o período.
- Cumulativo = Seu valor será False se precisarmos da ocorrência exata de um evento e True se um número de eventos aleatórios estiver entre 0 e esse evento.

A distribuição de Poisson é calculada usando a fórmula do excel
Artigos recomendados
Este foi um guia para a fórmula de distribuição de Poisson. Aqui discutimos Como calcular a distribuição de Poisson, juntamente com exemplos práticos. Nós também fornecemos uma Calculadora de Distribuição de Poisson com um modelo de Excel para download. Você também pode consultar os seguintes artigos para saber mais -
- Calculadora para fórmula de distribuição normal padrão
- Cálculo da fórmula de distribuição T com modelo do Excel
- Fórmula para calcular a análise de variação
- O que é a fórmula de valor do ativo líquido?