
Introdução ao algoritmo DFS
O DFS é conhecido como o algoritmo de profundidade da primeira pesquisa, que fornece as etapas para percorrer todos os nós de um gráfico sem repetir nenhum nó. Esse algoritmo é o mesmo que o Profundidade da primeira travessia para uma árvore, mas difere em manter um booleano para verificar se o nó já foi visitado ou não. Isso é importante para a travessia do gráfico, pois também existem ciclos no gráfico. Uma pilha é mantida neste algoritmo para armazenar os nós suspensos durante a travessia. É assim chamado porque primeiro viajamos para a profundidade de cada nó adjacente e depois continuamos atravessando outro nó adjacente.
Explique o algoritmo DFS
Esse algoritmo é contrário ao algoritmo BFS, no qual todos os nós adjacentes são visitados, seguidos pelos vizinhos dos nós adjacentes. Ele começa a explorar o gráfico a partir de um nó e explora sua profundidade antes de voltar atrás. Duas coisas são consideradas neste algoritmo:
- Visitando um vértice: seleção de um vértice ou nó do gráfico a percorrer.
- Exploração de um vértice: atravessando todos os nós adjacentes a esse vértice.
Pseudo-código para a primeira pesquisa de profundidade :
proc DFS_implement(G, v):
let St be a stack
St.push(v)
while St has elements
v = St.pop()
if v is not labeled as visited:
label v as visited
for all edge v to w in G.adjacentEdges(v) do
St.push(w)
O Traversal linear também existe para o DFS que pode ser implementado de três maneiras:
- Pedido antecipado
- Em ordem
- PostOrder
A ordem posterior inversa é uma maneira muito útil de percorrer e usada na classificação topológica, bem como em várias análises. Uma pilha também é mantida para armazenar os nós cuja exploração ainda está pendente.
Percurso do gráfico no DFS
No DFS, as etapas abaixo são seguidas para percorrer o gráfico. Por exemplo, em um determinado gráfico, vamos começar a travessia de 1:
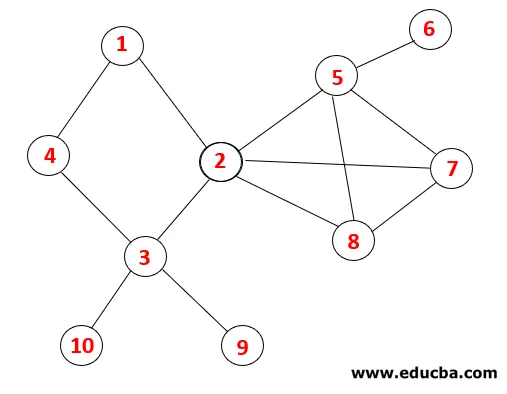
| Pilha | Sequência transversal | Spanning Tree |
| 1 1 |  |
|
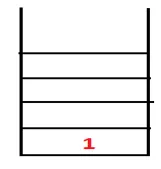 | 1, 4 |  |
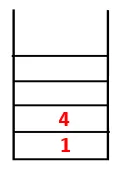 | 1, 4, 3 |  |
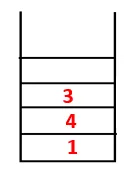 | 1, 4, 3, 10 | 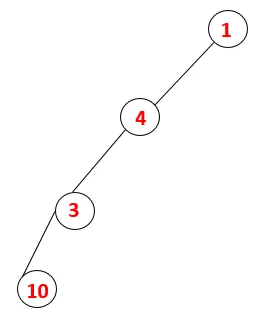 |
 | 1, 4, 3, 10, 9 | 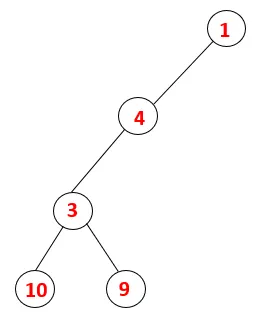 |
 | 1, 4, 3, 10, 9, 2 | 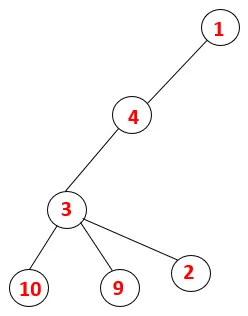 |
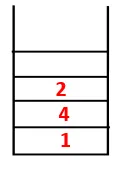 | 1, 4, 3, 10, 9, 2, 8 |  |
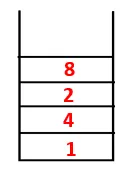 | 1, 4, 3, 10, 9, 2, 8, 7 | 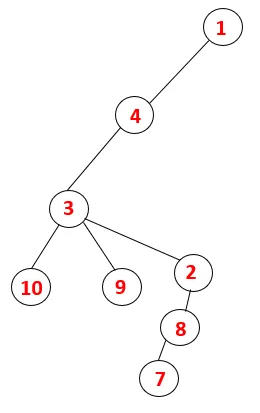 |
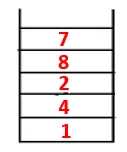 | 1, 4, 3, 10, 9, 2, 8, 7, 5 |  |
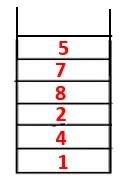 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 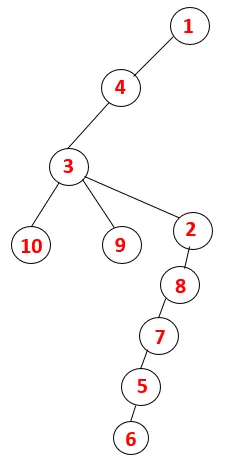 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 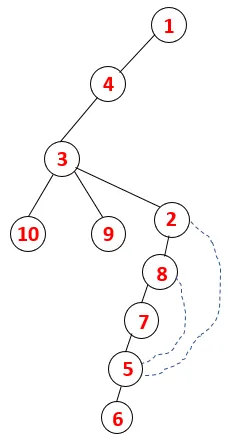 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
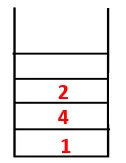 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 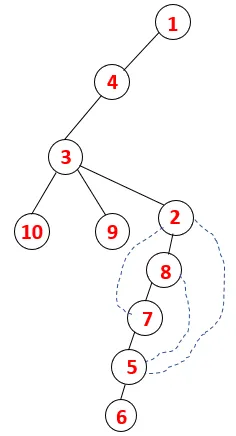 |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 |  |
 | 1, 4, 3, 10, 9, 2, 8, 7, 5, 6 | 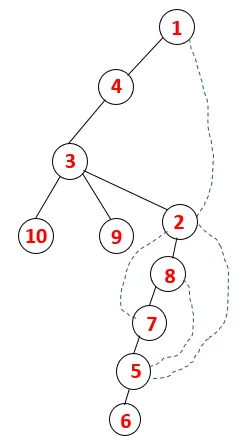 |
Explicação para o algoritmo DFS
Abaixo estão as etapas para o algoritmo DFS com vantagens e desvantagens:
Etapa 1: o nó 1 é visitado e adicionado à sequência e à árvore de expansão.
Etapa 2: os nós adjacentes de 1 são explorados, sendo 4, sendo 1 empurrado para empilhar e 4 empurrado para a sequência e para a árvore de abrangência.
Etapa 3: Um dos nós adjacentes de 4 é explorado e, assim, 4 é empurrado para a pilha e 3 entra na sequência e na árvore de abrangência.
Etapa 4: nós adjacentes de 3 são explorados empurrando-o para a pilha e 10 entra na sequência. Como não há nó adjacente a 10, assim 3 é retirado da pilha.
Etapa 5: Outro nó adjacente de 3 é explorado e 3 é empurrado para a pilha e 9 é visitado. Nenhum nó adjacente de 9, portanto, 3 é exibido e o último nó adjacente de 3, ou seja, 2 é visitado.
Processo semelhante é seguido para todos os nós até que a pilha fique vazia, o que indica a condição de parada para o algoritmo transversal. - -> linhas pontilhadas na árvore de abrangência se referem às arestas traseiras presentes no gráfico.
Dessa forma, todos os nós no gráfico são deslocados sem repetir nenhum dos nós.
Vantagens e desvantagens
- Vantagens: Este requisito de memória para este algoritmo é muito menor. Menor complexidade de espaço e tempo que o BFS.
- Desvantagens: A solução não é garantida. Classificação topológica. Encontrando pontes de gráfico.
Exemplo para implementar o algoritmo DFS
Abaixo está o exemplo para implementar o algoritmo DFS:
Código:
import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)import java.util.Stack;
public class DepthFirstSearch (
static void depthFirstSearch(int()() matrix, int source)(
boolean() visited = new boolean (matrix.length);
visited(source-1) = true;
Stack stack = new Stack();
stack.push(source);
int i, x;
System.out.println("Depth of first order is");
System.out.println(source);
while(!stack.isEmpty())(
x= stack.pop();
for(i=0;i if(matrix(x-1)(i) == 1 && visited(i) == false)(
stack.push(x);
visited(i)=true;
System.out.println(i+1);
x=i+1;
i=-1;
)
)
)
)
public static void main(String() args)(
int vertices=5;
int()() mymatrix = new int(vertices)(vertices);
for(int i=0;i for(int j=0;j mymatrix(i)(j)= i+j;
)
)
depthFirstSearch(mymatrix, 5);
)
)
Resultado:
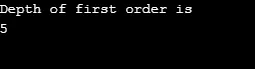
Explicação para o programa acima: Criamos um gráfico com 5 vértices (0, 1, 2, 3, 4) e usamos a matriz visitada para acompanhar todos os vértices visitados. Em seguida, para cada nó cujos nós adjacentes existem, o mesmo algoritmo se repete até que todos os nós sejam visitados. Em seguida, o algoritmo volta a chamar o vértice e o tira da pilha.
Conclusão
O requisito de memória deste gráfico é menor quando comparado ao BFS, pois apenas uma pilha é necessária para ser mantida. Uma árvore de abrangência DFS e uma seqüência de travessia são geradas como resultado, mas não são constantes. A sequência transversal múltipla é possível, dependendo do vértice inicial e do vértice de exploração escolhido.
Artigos recomendados
Este é um guia para o algoritmo DFS. Aqui discutimos a explicação passo a passo, percorremos o gráfico em um formato de tabela com vantagens e desvantagens. Você também pode consultar nossos outros artigos relacionados para saber mais -
- O que é o HDFS?
- Algoritmos de Aprendizagem Profunda
- Comandos HDFS
- Algoritmo SHA