
Fórmula Média (Sumário)
- Fórmula Média
- Exemplos de fórmula média (com modelo do Excel)
- Mean Formula Calculator
Fórmula Média
Mean é um ponto em um conjunto de dados que é a média de todos os pontos de dados que temos em um conjunto. É basicamente a média aritmética do conjunto de dados e pode ser calculada pegando uma soma de todos os pontos de dados e depois dividindo-o pelo número de pontos de dados que temos no conjunto de dados. Nas estatísticas, a média é o método mais comum para medir o centro de um conjunto de dados. É uma parte muito básica, mas importante, da análise estatística dos dados. Se calcularmos o valor médio do conjunto da população, isso será chamado de média da população. Mas às vezes o que acontece é que os dados da população são muito grandes e não podemos realizar análises nesse conjunto de dados. Portanto, nesse caso, extraímos uma amostra e fazemos uma média. Essa amostra representa basicamente o conjunto da população e a média é chamada de média da amostra. Valor médio é o valor médio que ficará entre o valor máximo e o mínimo no conjunto de dados, mas não será o número no conjunto de dados.
Uma fórmula para Média é dada por:
Mean = Sum of All Data Points / Number of Data Points
Existe outra maneira de calcular a média que não é muito usada. É chamado método da média assumida. Nesse método, um valor aleatório é selecionado no conjunto de dados e assumido como médio. Em seguida, o desvio dos pontos de dados desse valor é calculado. Portanto, a média é dada por:
Mean = Assumed Mean + (Sum of All Deviations / Number of Data Points)
Exemplos de fórmula média (com modelo do Excel)
Vamos dar um exemplo para entender melhor o cálculo da fórmula Média.
Você pode fazer o download deste modelo médio aqui - Modelo médioFórmula Média - Exemplo # 1
Digamos que você tenha um conjunto de dados com 10 pontos de dados e queremos calcular a média para isso.
Conjunto de dados: (4, 6, 8, 9, 22, 83, 98, 45, 87, 10)
Solução:
A média é calculada usando a fórmula abaixo
Média = soma de todos os pontos de dados / número de pontos de dados
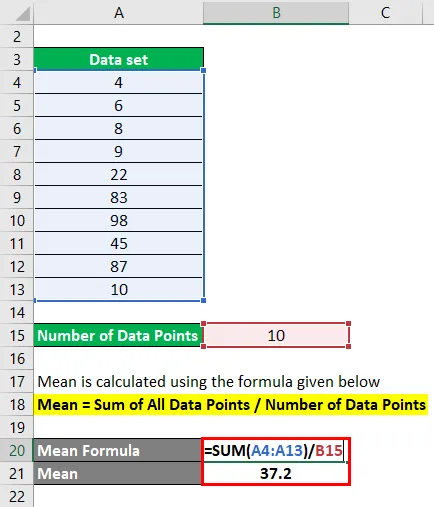
- Média = (4 + 6 + 8 + 9 + 22 + 83 + 98 + 45 + 87 + 10) / 10
- Média = 372/10
- Média = 37, 2
Vamos usar o método Média Assumida para encontrar média no mesmo exemplo.
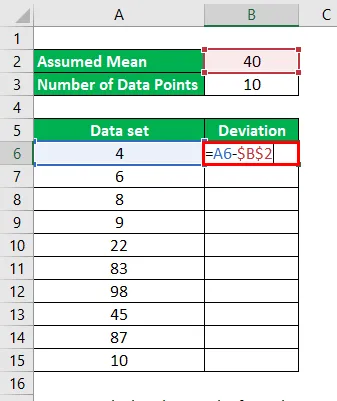
Vamos supor que a média para o conjunto de dados fornecido seja 40. Portanto, os desvios serão calculados como:
Para o primeiro ponto de dados, 4 - 40 = -36
O resultado será o indicado abaixo.
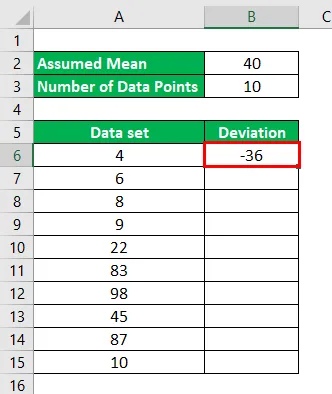
Da mesma forma, temos que calcular o desvio para todos os pontos de dados.
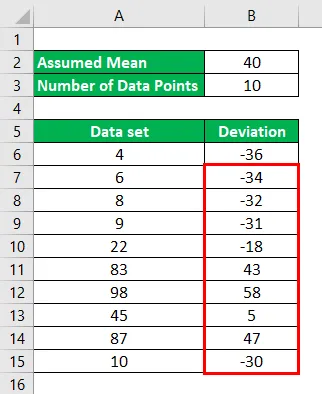
A média é calculada usando a fórmula abaixo
Média = Média Assumida + (Soma de Todos os Desvios / Número de Pontos de Dados)
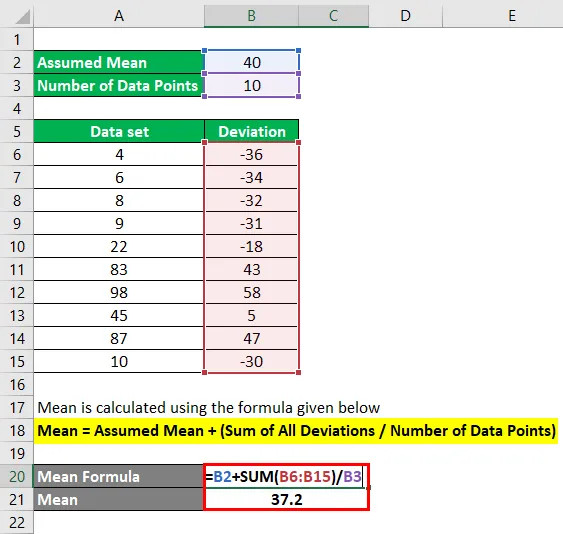
- Média = 40 + (-36 -34-32-31-18 + 43 + 58 + 5 + 47-30) / 10
- Média = 40 + (-28) / 10
- Média = 40 + (-2, 8)
- Média = 37, 2
Fórmula Média - Exemplo # 2
Vamos fazer um balanço das ações da IBM e tomaremos seus preços históricos dos últimos 10 meses e calcularemos o retorno anual de 10 meses.
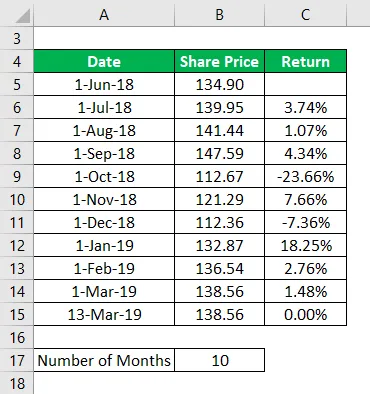
Link da fonte: https://in.finance.yahoo.com/quote/IBM/
Solução:
A média é calculada usando a fórmula abaixo
Média = soma de todos os pontos de dados / número de pontos de dados
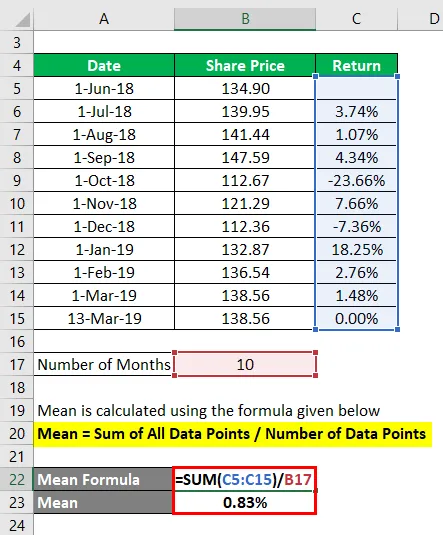
- Média = (3, 74% + 1, 07% + 4, 34% + (-23, 66)% + 7, 66% + (-7, 36)% + 18, 25% + 2, 76% + 1, 48% + 0, 00%) / 10
- Média = 8, 28% / 10
- Média = 0, 83%
Portanto, se você vê aqui, nos últimos 10 meses, o retorno da IBM flutuou muito.
No geral, nos últimos 10 meses, o retorno médio é de apenas 0, 83%
Explicação
A média é basicamente uma média simples dos pontos de dados que temos em um conjunto de dados e nos ajuda a entender o ponto médio do conjunto de dados. Mas existem certas limitações no uso da média. O valor médio é facilmente distorcido por valores extremos / outliers. Esses valores extremos podem ser muito pequenos ou muito grandes, o que pode distorcer a média. Por exemplo: Digamos que tenhamos retornos de estoque nos últimos 5 anos, dados em 5%, 2%, 1%, 5%, -30%. A média desses valores é de -3, 4% ((5 + 2 + 1 + 5-30) / 5). Portanto, embora o estoque tenha proporcionado um retorno positivo nos primeiros 4 anos, em média, temos uma média negativa de 3, 4%. Da mesma forma, se tivermos um projeto para o qual estamos analisando o fluxo de caixa nos próximos 5 anos. Digamos que os fluxos de caixa sejam: -100, -100, -100, -100, +1000.
A média é 600/5 = 120. Embora tenhamos uma média positiva, só estamos recebendo dinheiro no ano passado do projeto e pode acontecer que, se incorporarmos o valor do dinheiro no tempo, esse projeto não parecerá tão lucrativo quanto agora .
Relevância e usos da fórmula média
A média é muito simples, mas um dos elementos cruciais da estatística. É a base básica da análise estatística de dados. É muito fácil de calcular e fácil de entender também. Se tivermos um conjunto de dados com pontos de dados espalhados por todo o lugar, o mean nos ajuda a ver qual é a média desse ponto de dados. Por exemplo: Se um estoque X tiver retornos dos últimos 5 anos como 20%, -10%, 3%, -7%, 30%. Se você ver todos os anos têm retornos diferentes. A média para isso é de 7, 2% ((20-10 + 3-7 + 30) / 5). Portanto, agora podemos simplesmente dizer que, em média, as ações nos deram um retorno anual de 7, 2%.
Mas se vemos a média em um silo, ela tem relativamente menos importância por causa das falhas discutidas acima e é mais um número teórico. Portanto, devemos usar o valor médio com muito cuidado e não devemos analisar os dados apenas com base na média.
Mean Formula Calculator
Você pode usar a seguinte calculadora média
| Soma de todos os pontos de dados | |
| Número de pontos de dados | |
| Fórmula Média | |
| Fórmula Média | = |
|
|
Artigos recomendados
Este foi um guia para a Fórmula Média. Aqui discutimos como calcular a média, juntamente com exemplos práticos. Também fornecemos à calculadora Mean um modelo de Excel para download. Você também pode consultar os seguintes artigos para saber mais -
- Cálculo da elasticidade do preço
- Guia para a fórmula do rácio de solvência
- Exemplos de fórmula de variação de portfólio
- Fórmula DPMO