Introdução ao Clustering Hierárquico
- Recentemente, um de nossos clientes solicitou à nossa equipe que apresentasse uma lista de segmentos com uma ordem de importância dentro de seus clientes para direcioná-los à franquia de um de seus produtos recém-lançados. Claramente, apenas segmentar os clientes usando cluster parcial (k-means, c-fuzzy) não trará à ordem de importância que é onde o cluster hierárquico entra em cena.
- O cluster hierárquico está separando os dados em diferentes grupos com base em algumas medidas de similaridade conhecidas como clusters, que visam essencialmente a construção da hierarquia entre os clusters. É basicamente um aprendizado não supervisionado e a escolha dos atributos para medir a similaridade é específica da aplicação.
O cluster da hierarquia de dados
- Clustering Aglomerativo
- Clustering divisivo
Vamos dar um exemplo de dados, notas obtidas por 5 alunos para agrupá-los para uma próxima competição.
| Aluna | Marcas |
| UMA | 10 |
| B | 7 |
| C | 28. |
| D | 20 |
| E | 35s |
1. Clustering Aglomerado
- Para começar, consideramos cada ponto / elemento individual aqui ponderado como clusters e continuamos a mesclar os pontos / elementos semelhantes para formar um novo cluster no novo nível, até ficarmos com o único cluster, uma abordagem de baixo para cima.
- Ligação única e ligação completa são dois exemplos populares de agrupamento aglomerativo. Diferente da ligação Média e da ligação Centroid. Em ligação única, mesclamos em cada etapa os dois grupos, cujos dois membros mais próximos têm a menor distância. Em ligação completa, fundimos os membros da menor distância que fornecem a menor distância máxima em pares.
- Matriz de proximidade, é o núcleo para a realização de cluster hierárquico, que fornece a distância entre cada um dos pontos.
- Vamos criar uma matriz de proximidade para os dados apresentados na tabela, pois, como estamos calculando a distância entre cada um dos pontos com outros pontos, será uma matriz assimétrica de forma n × n, no nosso caso, matrizes 5 × 5.
Um método popular para cálculos de distância são:
- Distância euclidiana (ao quadrado)
dist((x, y), (a, b)) = √(x - a)² + (y - b)²
- Distância Manhattan
dist((x, y), (a, b)) =|x−c|+|y−d|
A distância euclidiana é mais comumente usada, usaremos a mesma aqui e seguiremos com ligação complexa.
| Estudante (Clusters) | UMA | B | C | D | E |
| UMA | 0 0 | 3 | 18 | 10 | 25 |
| B | 3 | 0 0 | 21 | 13 | 28. |
| C | 18 | 21 | 0 0 | 8 | 7 |
| D | 10 | 13 | 8 | 0 0 | 15 |
| E | 25 | 28. | 7 | 15 | 0 0 |
Os elementos diagonais da matriz de proximidade serão sempre 0, pois a distância entre o ponto com o mesmo ponto será sempre 0, portanto, os elementos diagonais são isentos de consideração para agrupamento.
Aqui, na iteração 1, a menor distância é 3, portanto, mesclamos A e B para formar um cluster, novamente formando uma nova matriz de proximidade com o cluster (A, B) assumindo (A, B) o ponto do cluster como 10, ou seja, no máximo ( 7, 10), então a matriz de proximidade recém-formada seria
| Clusters | (A, B) | C | D | E |
| (A, B) | 0 0 | 18 | 10 | 25 |
| C | 18 | 0 0 | 8 | 7 |
| D | 10 | 8 | 0 0 | 15 |
| E | 25 | 7 | 15 | 0 0 |
Na iteração 2, 7 é a distância mínima, portanto, como mesclamos C e E formando um novo cluster (C, E), repetimos o processo seguido na iteração 1 até terminarmos com o cluster único, aqui paramos na iteração 4.
Todo o processo está representado na figura abaixo:
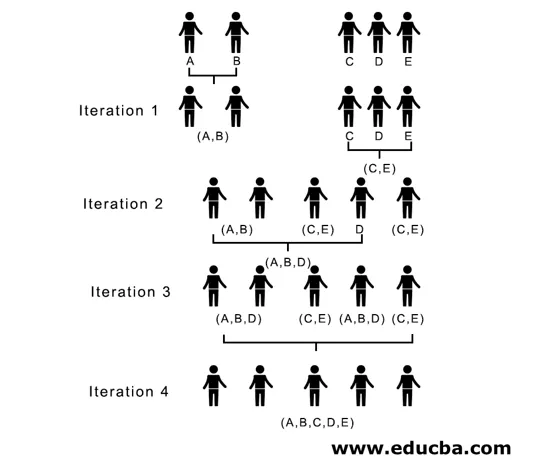
(A, B, D) e (D, E) são os 2 clusters formados na iteração 3; na última iteração, podemos ver que resta um único cluster.
2. Clustering Divisivo
Para começar, consideramos todos os pontos como um único agrupamento e os separamos pela maior distância até terminarmos com pontos individuais como agrupamentos individuais (não necessariamente podemos parar no meio, depende do número mínimo de elementos que queremos em cada agrupamento) em cada etapa. É exatamente o oposto do agrupamento aglomerado e é uma abordagem de cima para baixo. Cluster divisivo é uma maneira repetitiva de k significa cluster.
A escolha entre Clustering Aglomerativo e Divisivo depende novamente da aplicação, mas poucos pontos a serem considerados são:
- A divisão é mais complexa do que o aglomerado.
- O armazenamento em cluster divisivo é mais eficiente se não gerarmos uma hierarquia completa até pontos de dados individuais.
- O agrupamento aglomerativo toma uma decisão considerando os padrões locais, sem levar em consideração os padrões globais inicialmente que não podem ser revertidos.
Visualização de cluster hierárquico
Um método super útil para visualizar o cluster hierárquico que ajuda nos negócios é o Dendogram. Os dendogramas são estruturas semelhantes a árvores que registram a sequência de mesclagens e divisões nas quais a linha vertical representa a distância entre os aglomerados, a distância entre as linhas verticais e a distância entre os aglomerados é diretamente proporcional, isto é, quanto maior a distância que os aglomerados provavelmente serão diferentes.
Podemos usar o dendograma para decidir o número de clusters, basta desenhar uma linha que cruza com uma linha vertical mais longa no dendograma, um número de linhas verticais cruzadas será o número de clusters a serem considerados.
Abaixo está o exemplo Dendograma.
Existem pacotes python bastante simples e diretos e suas funções para executar cluster hierárquico e dendogramas de plotagem.
- A hierarquia do scipy.
- Cluster.hierarchy.dendogram para visualização.
Cenários comuns em que o cluster hierárquico é usado
- Segmentação de clientes para marketing de produtos ou serviços.
- Planejamento da cidade para identificar os locais para construir estruturas / serviços / construção.
- A análise de redes sociais, por exemplo, identifica todos os fãs de MS Dhoni para anunciar sua biografia.
Vantagens do cluster hierárquico
As vantagens são dadas abaixo:
- No caso de clustering parcial como k-means, o número de clusters deve ser conhecido antes do clustering, o que não é possível em aplicações práticas, enquanto que no clustering hierárquico não é necessário conhecimento prévio do número de clusters.
- O cluster hierárquico gera uma hierarquia, ou seja, uma estrutura mais informativa que o conjunto não estruturado dos clusters planos retornados pelo cluster parcial.
- O armazenamento em cluster hierárquico é fácil de implementar.
- Apresenta resultados na maioria dos cenários.
Conclusão
O tipo de cluster faz a grande diferença quando os dados estão sendo apresentados, sendo o cluster hierárquico mais informativo e fácil de analisar, mais preferido do que o cluster parcial. E é frequentemente associado a mapas de calor. Não esquecer os atributos escolhidos para calcular a similaridade ou dissimilaridade influencia predominantemente os clusters e a hierarquia.
Artigos recomendados
Este é um guia para cluster hierárquico. Aqui discutimos a introdução, vantagens do cluster hierárquico e cenários comuns nos quais o cluster hierárquico é usado. Você também pode consultar nossos outros artigos sugeridos para saber mais:
- Algoritmo de cluster
- Clustering no Machine Learning
- Clustering hierárquico em R
- Métodos de agrupamento
- Como remover a hierarquia no Tableau?