Introdução ao algoritmo de cluster hierárquico
O algoritmo de agrupamento hierárquico é uma técnica de aprendizado de máquina não supervisionada. O objetivo é encontrar agrupamentos naturais com base nas características dos dados.
O algoritmo de cluster hierárquico visa encontrar grupos aninhados de dados construindo a hierarquia. É semelhante à taxonomia biológica do reino vegetal ou animal. Clusters hierárquicos são geralmente representados usando a árvore hierárquica conhecida como dendrograma.
Tipos de algoritmo de cluster hierárquico
Os algoritmos de cluster hierárquicos são de 2 tipos:
- Divisivo
- Aglomerativo
1. Divisivo
Essa é uma abordagem de cima para baixo, na qual considera inicialmente os dados inteiros como um grupo e, em seguida, divide os dados em subgrupos. Se o número de um algoritmo de cluster hierárquico for conhecido, o processo de divisão será interrompido quando o número de clusters for alcançado. Senão, o processo para quando os dados não podem mais ser divididos, o que significa que o subgrupo obtido da iteração atual é o mesmo que o obtido na iteração anterior (também é possível considerar que a divisão para quando cada ponto de dados é um cluster )
2. Aglomerado
É uma abordagem de baixo para cima que se baseia na mesclagem de clusters. Inicialmente, os dados são divididos em m clusters singleton (em que o valor de m é o número de amostras / pontos de dados). Dois clusters são mesclados em um iterativamente, reduzindo assim o número de clusters em cada iteração. Esse processo de mesclagem de clusters é interrompido quando todos os clusters foram mesclados em um ou o número de clusters desejados é alcançado.
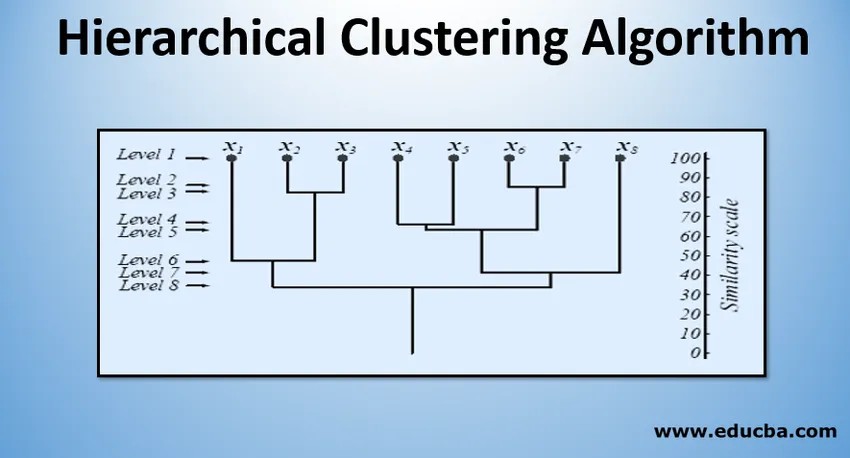
No nível 1, existem m clusters que são reduzidos para 1 cluster no nível m. Os pontos de dados que são mesclados para formar um cluster em um nível mais baixo também ficam no mesmo cluster nos níveis mais altos. Por exemplo, suponha que existam 8 pontos x1..x8, portanto, inicialmente, existem 8 clusters no nível 1. Suponha que os pontos x1 e x2 sejam mesclados em um cluster no nível 2 e, até o nível 8, eles permaneçam no mesmo cluster.
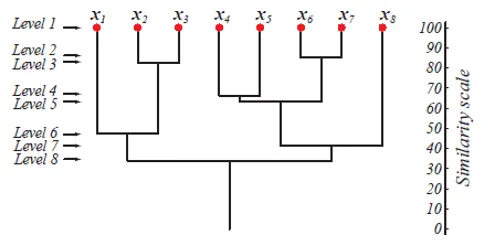
A figura acima mostra uma representação em dendrograma da abordagem de aglomeração em cluster para 8 pontos de dados, bem como a escala de similaridade correspondente a cada nível.
Os níveis de clusters nos dão uma idéia de quão semelhantes são os pontos de dados nos clusters. Como mostra a figura 1, anteriormente os pontos de dados são mesclados em um cluster, os mesmos são. Portanto, os pontos de dados em um cluster no nível 2 (por exemplo, x2 e x3) são mais semelhantes que os pontos de dados em um cluster no nível 6 (por exemplo, x1 e x2).
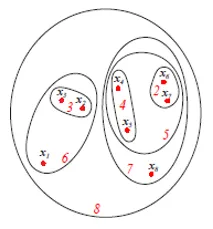
A figura acima mostra a representação do diagrama de Set ou Venn da abordagem de agrupamento aglomerado dos 8 pontos de dados acima mencionados. Tanto os dendogramas quanto as representações de conjuntos podem ser usados para armazenamento em cluster. No entanto, um dendograma é geralmente preferível, a representação de ativos não pode representar quantitativamente as semelhanças do cluster.
Etapas para o algoritmo de cluster hierárquico
Vamos seguir as seguintes etapas para o algoritmo de cluster hierárquico que são fornecidas abaixo:
1. Algoritmo
Algoritmo de cluster hierárquico aglomerativo
- Comece a inicializar c, c1 = n, Di = (xi), i = 1, …, n '
- Faça c1 = c1 - 1
- Encontre os clusters mais próximos, digamos, Di e Dj
- Mesclar Di e Dj
- Até c = c1
- Retornar clusters c
- Fim
Esse algoritmo começa com n clusters inicialmente onde cada ponto de dados é um cluster. A cada iteração, o número de clusters reduz em 1 à medida que os 2 clusters mais próximos são mesclados. Esse processo continua até que o número de clusters seja reduzido ao valor predefinido c.
Como decidir quais clusters estão próximos?
Isso é definido usando várias métricas de distância, que são as seguintes:
- A distância mínima entre os clusters dmin (Di, Dj). Útil para solteiro.
- A distância máxima entre os clusters dmax (Di, Dj). Útil para completar.
- A distância média entre os clusters davg (Di, Dj).
O que é ligação única e ligação completa?
- Quando dmin (di, dj) é usado para encontrar a distância entre dois clusters, e o algoritmo termina se a distância entre os clusters mais próximos exceder um limite, o algoritmo será chamado de algoritmo de ligação única.
- Quando dmax (Di, Dj) é usado para encontrar a distância entre dois clusters, e o algoritmo termina se a distância entre os clusters mais próximos exceder um limite, então o algoritmo é chamado de algoritmo de ligação completo.
- Vamos considerar cada ponto de dados como um nó de um gráfico. Há uma aresta entre dois pontos de dados se eles pertencerem ao mesmo cluster. Quando dois clusters mais próximos são mesclados, uma aresta é adicionada. É chamado de ligação única porque existe um caminho exclusivo de um nó para o outro.
- O algoritmo de ligação completo mescla dois clusters, minimizando a distância entre os dois pontos mais distantes.
- Um algoritmo de ligação única gera uma árvore de abrangência. No entanto, esse algoritmo é suscetível a ruído. Um algoritmo de ligação completo gera um gráfico completo.
Qual é a complexidade temporal do algoritmo?
Suponha que temos n padrões no espaço d-dimensional e usamos dmin (Di, Dj) para formar clusters c. Precisamos calcular n (n - 1) distâncias entre pontos - cada uma das quais é um cálculo de O (d2) - e colocar os resultados em uma tabela de distâncias entre pontos. A complexidade do espaço é O (n 2 ). Para encontrar o par mínimo de distância (para a primeira mesclagem), é necessário percorrer a lista completa, mantendo o índice da menor distância.
Assim, para a primeira etapa aglomerativa, a complexidade é O (n (n - 1) (d 2 + 1)) = O (n 2 d 2 ). Para outra etapa de aglomeração arbitrária (ou seja, de c1 a c1 - 1), apenas percorremos as distâncias n (n - 1) - c1 “não utilizadas” da lista e encontramos a menor para a qual x e x 'estão em diferentes aglomerados . Este é, novamente, O (n (n-1) -c1). A complexidade total do tempo é, portanto, O (cn 2 d 2 ) e, em condições típicas, n >> c.
2. Visualização
Depois que os dados são divididos em clusters, é uma boa prática visualizá-los para ter uma idéia de como é o agrupamento. Mas visualizar esses dados de alta dimensão é difícil. Portanto, usamos a Análise de Componentes Principais (PCA) para visualização. Após o PCA, obtemos os pontos de dados no espaço de baixa dimensão (geralmente 2D ou 3D) que podemos plotar para ver o agrupamento.
Nota: Dimensão alta significa um grande número de recursos e não um número de pontos de dados.3. Avaliação
Um dos métodos para a avaliação de clusters é que a distância dos pontos entre os clusters (distância entre clusters) deve ser muito maior que a distância dos pontos dentro do cluster (distância entre clusters).
Conclusão
A seguir, são apresentados alguns dos principais argumentos:
- O algoritmo de cluster hierárquico é usado para encontrar padrões aninhados em dados
- O agrupamento hierárquico é de 2 tipos - Divisivo e Aglomerativo
- Dendrograma e diagrama de set / Venn podem ser usados para representação
- A ligação única mescla dois clusters, minimizando a distância mínima entre eles. Forma uma extensão
- A ligação completa mescla dois clusters, minimizando a distância máxima entre ele e forma um gráfico completo.
- A complexidade do tempo total do algoritmo de cluster hierárquico é O (cn 2 d 2 ), onde c é o número predefinido de clusters, n é o número de padrões ed é o espaço d-dimensional dos n padrões.
Artigos recomendados
Este é um guia para o algoritmo Hierarchical Clustering. Aqui discutimos os tipos e etapas dos algoritmos de cluster hierárquico. Você também pode consultar os seguintes artigos para saber mais:
- Análise de cluster hierárquica
- Clustering hierárquico em R '
- Algoritmo de cluster
- O que é clustering na mineração de dados?
- Clustering hierárquico | Clustering Aglomerativo e Divisivo
- Algoritmo C ++ | Exemplos de algoritmo C ++